(Харьков – 1985 г.)
Оглавление:
I. Аксиоматический метод теоретизирования.
II. Эволюционное теоретизирование.
II.1. Интеллектуальные структуры Ж. Пиаже.
II.2. Стадии развития морали по Л. Колбергу.
II.3. Эволюционная формализация Д.В. Осадчего.
III. Дальнейшее развитие представлений об эволюционной формализации у Д.В. Осадчего.
IV. Эволюционная формализация как дальнейшее развитие теории познания.
V. Законы сохранения – инварианты разных уровней развития.
VI. Энтропия – функция состояния данного уровня развития.
VII. Следствия и примеры для естествоиспытателя.
Литература
ДОПОЛНИТЕЛЬНЫЕ ЗАМЕЧАНИЯ О МЕТОДЕ ЭВОЛЮЦИОННОЙ ФОРМАЛИЗАЦИИ
Оглавление:
VIII. О типах научного знания.
IX. Типы научного знания в связи со схемой Н.А.Бернштейна.
X. Три принципа познания ХХ века.
XI. Каким образом разные типы знания входят в культуру?
XII. Что такое теоретическая биология?
XIII. Как изменяется педагогическая задача при переходе со структурного уровня на организационный
Литература

Д.В.Осадчий (1956 – 1984)
« Жизнь не окончена пока,
Ржавеет бритва у Оккама,
А на столе лежит программа
Мероприятий на века...»
(Д.В. Осадчий)
Дмитрий Владимирович Осадчий (1956 – 1984) был гением. Он был поэтом, актером народного театра, художником, автором и исполнителем своих песен. За свою короткую научную жизнь он успел оставить неповторимый след в химии, физике, теории музыки, математике, философии благодаря тому, что создал оригинальный метод теоретизирования, который он назвал «методом эволюционной формализации». И в каждой решаемой им проблеме он занимался развитием и совершенствованием этого метода. После его трагической гибели остались только разрозненные записи, конспекты немногих лекций, которые он читал маленькой аудитории (в состав которой входил и автор этого очерка). Я сделал попытку, опираясь на эти материалы, как можно более связно изложить сущность его метода познания и описания развивающихся объектов – метода эволюционной формализации.
Харьков, январь 1985 г.
I. Аксиоматический метод теоретизирования.
Способ теоретизирования, идеал "хорошей" теории различны в разные периоды развития науки и определяются природой той части реального мира, которой интересуется наука в данный период времени. Теории, созданные для описания объектов, принадлежащих этой реальности, становятся доминирующими в соответствующую эпоху, они определяют интеллектуальную атмосферу эпохи и автоматически применяются к описанию и тех объектов, которые по своей природе относятся совсем к другой области реальности. Более или менее удовлетворительное (в зависимости от соответствия природе объектов) описание данным теоретическим способом известного науке мира представляет собой научную картину мира данной эпохи. Этот образ "научности" закрепляется в сознании исследователей, и любые объекты, попадающие с течением времени в поле зрения науки, для того, чтобы быть «понятыми научно» должны быть описаны принятым способом. При этом часто возникают искаженные представления о целых областях реальности, что проявляется в громоздкости и явной искусственности теоретических построений (например, система мира по Птоломею), а по мере все более глубокого изучения новых реальностей выявляются противоречия между фактами и научным описанием объектов (как это было, например, с теорией эфира ХХ века), что в конце концов приводит к ломке старого способа описания. Происходит смена парадигмы (по Т. Куну) в науке.
Появляется новый способ теоретизирования, который соответствует природе объектов новых областей реальности: в соответствии с новым способом теоретизирования заново описываются и старые объекты – изменяется способ их видения (в физике это называется принципом соответствия). Так в науке Нового времени господствовала механика и ко всем другим объектам реальности (объектам других областей физики и объектам других разделов естествознания) применялся механистический способ описания. Этот способ развивался в тесной связи с математикой, с аксиоматико – дедуктивным способом ее построения. Со времени Галилея идеалом теоретического описания мира является определенная система аксиом, полученная как результат экспериментального исследования природы, и системы теорем, выводимых логико – дедуктивным методом из этих аксиом. Выводы теории проверяются экспериментом. Таким образом степень соответствия наблюдаемых и теоретически выводимых свойств объектов от положенной в основание теории системы аксиом (надо отметить, что в состав принимаемых аксиом неявно входят и законы формальной логики, по которым осуществляется вывод теорем).
В естествознании в качестве аксиом выступают эмпирические обобщения (В.И. Вернадский), производимые исследователем в конкретной области явлений природы, поэтому они в большой степени зависят от познавательной установки исследователя, его способа видения эмпирического материала, от того, какие свойства исследуемого объекта он считает существенными, а какие нет. До тех пор, пока наука имела дело с достаточно простыми (характеризующимися небольшим набором качеств) и неизменными объектами (время релаксации которых много больше времени экспериментального наблюдения за ними) – а как раз этим условиям удовлетворяли объекты классической механики – аксиоматический способ описания был достаточно корректен. Т.е., разные исследователи имели возможность ставить одни и те же эксперименты и получать одни и те же результаты независимо от того, кто, когда и где конкретно проводит опыт. А значит, и аксиомы, полученные как эмпирические обобщения опытных данных, и теоремы, выводимые из этих аксиом путем формально – логических рассуждений, были едины для всех исследователей и всех времен.
Но по мере расширения процесса познания, появления новых областей исследования наука сталкивалась с новыми объектами, описание которых приводило к необходимости как введения новых понятий, так и к расширению смысловой нагрузки старых. Примером последнего может служить изменение смысла понятия "масса" в процессе познания ?1?:
Масса – количество вещества.
– мера инерции тела.
– мера гравитационного воздействия.
– мера кинетической энергии.
– мера энергии связи.
"Каждый новый смысл разрушает предыдущую аксиоматику, ибо новое свойство не выводится на основании ранее сделанных допущений"?1?. Таким образом, по мере своего расширения, наука представляла собой все более многочисленный набор аксиоматически построенных теорий, являющихся как бы различными срезами реальности, сделанными в различных ее областях, но одним и тем же способом.
Когда наука перешла к изучению сложных и изменяющихся с течением времени объектов, попытки формального описания их аксиоматическим методом стали приводить к появлению большого числа неперекрывающихся описаний таких объектов, ни одно из которых не могло претендовать на полноту описания. Такое положение характерно для современной биологии ?см., например 2.?. Поскольку в науке идеалом теории по-прежнему считается теория аксиоматического типа (такая теория соответствует структуре математических теорий, а значит может быть математизирована), то в такой области знания, как биология, продолжаются поиски "наиболее полной" системы аксиом, на основании которой объект описывался бы исчерпывающе. При этом каждый автор считает именно свой подход к выделению наиболее существенных закономерностей объекта исследования правильным, руководствуясь при этом своим научным опытом, своей научной интуицией.
Не лучше ли признать, что порочность теоретических описаний сложных и развивающихся объектов заключается в том, что сам метод
теоретизирования неадекватен объекту описания? Наука расширилась и выросла многими своими областями за рамки того способа описания, который утвердила в ней классическая механика.А между тем существует альтернатива аксиоматическому методу теоретизирования.
II. Эволюционное теоретизирование.
Достаточно привести в качестве примера диалектический способ рассуждений, позволивший столь успешно решить задачу теоретического описания сложного и развивающегося объекта – социального организма, что было выполнено К.Марксом еще в прошлом веке. Существуют и более поздние попытки создания средств описания развивающихся объектов сложной природы. Наиболее интересный пример – работы Жана Пиаже по созданию операциональной теории мышления – «генетической эпистемологии».
1. Интеллектуальные структуры Ж. Пиаже.
(по В.Н. Чудакову [3, стр.15])
По Пиаже логика представляет собой аксиоматику сформировавшегося мышления. Тогда психология, изучающая становление и развитие мышления, предстает в качестве науки, прослеживающей становление аксиоматизированного мышления. Главный элемент психической деятельности – операции. Пиаже удалось построить психологическую теорию операций, базирующуюся на их генезисе и развитии в целостные структуры (представляющие собой, как уже говорилось выше, системы аксиом мышления).
С точки зрения психологии, операции – это действия, которые перенесены внутрь сознания, или интериоризированы. Ж.Пиаже называет их интериоризированными действиями. Такие операции стали обратимыми в противоположность реальным действиям, которые необратимы. Операции не существуют изолированно, их системы связаны в форме структурированного целого. В формировании операциональных структур интеллекта от рождения до зрелости, согласно Пиаже, можно выделить четыре основные стадии:
I стадия. Сенсомоторный период (0 – 2 года).
Этот период дооперационального интеллекта, действия ребенка еще не перенесены вовнутрь. Действия рефлекторны в ответ на воздействия внешней среды.
II стадия. Дооперациональная стадия (от 2 до 7 лет).
На базе символической функции – язык, символическая игра, отсроченная имитация и др. - становится возможной интериоризация действия в мысль.
III стадия. Конкретные операции (7 – 11 лет).
Различные типы мыслительной деятельности становятся обратимыми. Только обратимые действия представляют собой операцию. Обратимость означает, что для каждой операции есть симметричная и противоположная ей операция, которая, уничтожая исходную операцию, как бы восстанавливает первоначальное состояние.
IV стадия. Пропозициональные или формальные операции (от 11 – 12 до 14 – 15 лет).
Содержанием заключительного периода развития интеллекта (т.е. периода формирования логики взрослого) являются операции над операциями (конкретными), что обусловливает становление структур этих операций второго рода уже как формальных. Таким образом, мир взрослого человека – это мир, в котором господствует потенциально – возможное, управляемое логической необходимостью (формальными операциями), а реальная действительность оказывается лишь частным случаем потенциального и целиком подчиняется ему. Источник логической необходимости – свойство целостности складывающихся на этом уровне структур формальных операций.
Нетрудно видеть, что именно на этом уровне развития должен находиться интеллект исследователя, создающего аксиоматическую теорию изучаемого объекта. Но тогда вслед за И.З. Цехмистро зададим вопрос: а к какому же уровню отнести интеллект, создающий теорию развивающегося объекта, интеллект самого Ж.Пиаже?
(Здесь и далее по И.З. Цехмистро [3, стр. 28 – 38]). «Пиаже характеризует свой собственный подход к анализу мышления как диалектический. А это и означает, что рефлексия над формальными структурами мышления стала возможной для него фактически только с точки зрения некоторого более высокого познавательного и мыслительного уровня, называемого им самим диалектическим. Иными словами, в силу абсолютной привязанности к законам собственного мышления человек ничего не знал бы о них, поскольку для этого нужно подняться над ними, что невозможно без некоторой релятивизации исходного состояния. Адаптация к обстоятельствам реальной жизни вынуждает человека к релятивизации формально – логического способа мышления и его элементов, к пониманию относительности любых формально – логических вполне строгих заключений, обусловленной фактической текучестью и изменчивостью той среды, из которой черпаются исходные посылки для их построения. Здесь мышление как бы парит над формально – логическими построениями и по своему существу диалектично.
Таким образом есть все основания для исследования дальнейшего развития интеллекта, отправляясь от уровня формальных операций как исходного. По-видимому в развитии интеллекта неизбежен переход к более высоким типам уравновешивания и продуцируемым ими структурам уже не формально – логического, а более высокого порядка.
Пиаже прав в том, что в генетическом развитии, в процессе становления интеллекта, стадия формальных операций является высшей и завершающей. Однако сформировавшийся интеллект имеет еще историю собственного развития (а не только лишь формирования, на исследовании которого исключительно сосредоточился Пиаже). И собственное развитие сформировавшегося интеллекта не может быть ни чем иным, как становлением диалектического мышления на базе релятивизации формально – логического. Причем новая ступень становления диалектического мышления хорошо "вписывается" в общую канву формирования и развития интеллектуальных структур». Итак, можно дополнить «лестницу Пиаже» пятой ступенью:
V стадия: Диалектическое мышление, обеспечивающее адаптацию релятивизированного формально – логического мышления к реальной (развивающейся) действительности.
Сходную попытку описания процесса развития морали у ребенка предпринял Лоренс Колберг.
2. Стадии развития морали по Л. Колбергу (цит. по [4])
I стадия. Ориентация на наказание и награду.
II стадия. Человеческие отношения рассматриваются так, как обмен товарами на рынке: ты испачкал мою тетрадку, я порву твою.
III стадия. Ориентация на хорошого мальчика, хорошую девочку. Ребенок на этой стадии убежден, что хорошее поведение приятно людям.
IV стадия. Уважение к законам, к порядку, к авторитету, к правилу. Человек поддерживает установившийся социальный порядок, правилом поведения считает выполнение своих обязанностей. Кажется, что это высшая ступень морального развития, но нет, есть еще и пятая стадия, и шестая.
V стадия. Человек стремится понять законы как условия общественной жизни, критически изучить их, он понимает относительность личных ценностей.
VI стадия. Человек ориентируется на универсальные этические принципы, самостоятельно выбирает их, стремится найти общие принципы справедливости.
Нетрудно увидеть соответствие в выделении стадиальности развития в случае "лестницы Пиаже", дополненной И.З. Цехмистро пятой ступенью, со случаем "лестницы Колберга". Это сходство метода описания различных развивающихся объектов, полученного различными авторами, говорит о существовании общего метода теоретизирования, который принадлежит к более высокой стадии развития мышления исследователя (пятая ступень в "лестнице Пиаже").
3. Эволюционная формализация Д.В. Осадчего
Еще до знакомства с работами Ж.Пиаже Д.В.Осадчий пытался сформулировать эволюционный подход к построению теории для описания различных развивающихся объектов. Его позиция была сформулирована им так: "При познании эволюционного по своей природе объекта, путь сознательного эволюционного построения содержательных формальных структур путем диалектического СИНТЕЗА – единственный может привести к построению адекватной теории" [1].
«"Эволюционная формализация" – это содержательный смысл законов диалектики применительно к конкретному объекту исследования: формальным системам»[1], то есть это построение формального описания развивающегося объекта путем последовательного осуществления диалектического синтеза набора понятий, характеризующих изучаемый объект, взятый на какой – то конкретной стадии своего развития. Т.е. сама формализация как бы повторяет путь, по которому развивался объект, и завершается построением формальной системы, описывающей объект тогда, когда она на этом пути диалектического синтеза достигнет той же степени сложности, что и описываемый объект. В этой точке формальная система адекватна изучаемому объекту, и его описание в рамках этой системы полно.
Осадчий сформулировал критерии четырех этапов, последовательное осуществление которых приводило к реализации эволюционного построения формального описания объекта [1]:
I этап. Поиск понятийной базы (3 – 4 понятия). Понятия для будущей формализации должны представлять собой неотъемлемые свойства объекта. Набор понятий должен быть противоречив (последнее требование является основанием для второго этапа).
II этап. Поиск бинарных взаимоотношений между понятиями (установление межпонятийных связей). Понятия, образующие понятийную базу, должны быть связаны универсальным внутренним образом, что является основанием для третьего этапа.
III этап. Поиск генезиса понятий, т.е. поиск формальной операции, порождающей каждое из понятий.
IV этап. Определение метапонятия (мета – после) через порождающую операцию. При удачном выборе понятийной базы возможна свертка последней к одному метапонятию, которое будет удовлетворять критериям первого этапа на следующем уровне развития объекта (поиск метапонятийной базы).
В любой формальной системе, описывающей объект на данном этапе его развития, можно выделить понятийную базу, которая позволит выполнить все четыре этапа, что будет знаменовать собой завершение рассматриваемой формальной системы и переход к формальной системе следующего этапа развития объекта. Нетрудно заметить сходство последовательности этапов "эволюционной формализации" Осадчего и ступеней "лестницы Пиаже". Операцией перехода со ступени на ступень у Пиаже является интериоризация, тождественная диалектическому синтезу, или, как называет его в данном случае Осадчий, «свертке понятий».
Осадчий проиллюстрировал работу алгоритма эволюционной формализации на примере объектов геометрии. Но, прежде чем привести этот пример, необходимо сказать о том новом обозначении размерности объектов геометрии, которое ввел Осадчий:
так, для обозначения размерности точки – нульмерного объекта в общепринятой терминологии – он ввел обозначение Т1 (точка); прямая – одномерный объект – будет обозначаться как Т2 и т.д., т.е. в его обозначениях объекты имеют размерность на единицу большую, чем в общепринятом обозначении. Соответственно, нульмерный (по Осадчему) объект, обозначаемый как Т0 = 1, является "пустотой", т.е. его размерность на единицу меньше, чем у точки Т1. В дальнейшем будет показана естественность такого способа обозначения.
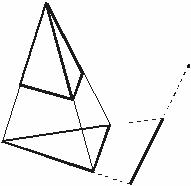
Рис. 1.
Теперь рассмотрим геометрический пример применения эволюционной формализации:
I этап: Содержательные понятия (понятийная база): точка, прямая, плоскость, тело.
II этап: Бинарные отношения между понятиями – в данном случае это граничные отношения: точка – граница отрезка прямой, прямая – граница плоской фигуры, плоскость – граница тела.
III этап: Порождающая операция для каждого из взятых понятий – операция взятия границы: конструкция этой операции – центральное проектирование (рис.1): проекция тела дает элемент плоскости, проекция элемента плоскости дает отрезок прямой, проекция отрезка дает точку.
Аналитически можно записать все эти геометрические объекты через операцию возведения точки Т в степень – это универсальная операция, связывающая всю понятийную базу. Будем возводить в степень N (N = 0; 1; 2...) выражение (1 + Т), т.е. точку плюс окружающую ее пустоту.
Получим: (1 + Т)0 = 1
(1 + Т)1 = 1 + Т
(1 + Т)2 = 1 + 2Т + Т2
(1 + Т)3 = 1 + 3Т + 3Т2 + Т3
(1 + Т)4 = 1 + 4Т + 6Т2 + 4Т3 + Т4
...........................................................
Коэффициенты в записи геометрических объектов через сумму их границ определяются биномиальным разложением. Интерпретировать такую запись легко, например: запись суммы границ для (1 + Т)3 означает, что объект, определяемый этой записью, имеет один элемент поверхности Т3, три элемента прямой Т2, три точки Т1, – легко догадаться, что этому описанию соответствует треугольник, а вообще запись через сумму границ с коэффициентами при членах, определяемыми по биномиальному разложению, в точности соответствует Рис.1, где изображены симплексы (т.е. простейшие объекты) различной размерности.
IV этап: Получаем метапонятие ТN – более общее определение геометрического пространства через порождающую операцию возведения в степень. Так, точка – Т1, прямая – Т2, плоскость – Т3, объем – Т4 и т.д.
Удачно проведенная эволюционная формализация дает возможность по-новому взглянуть на некоторые проблемы – это называется трактовкой частностей (V этап). Пример трактовки частностей: Эйлерова характеристика. Для любого выпуклого многогранника справедливо соотношение: В + Г = Р + 2, где В – количество вершин (Т1 в нашей записи); Г – количество граней (Т3); Р – количество ребер (Т2). Каков же смысл двойки?
Разложение многогранника по его границам позволяет объяснить смысл этой двойки: 2 = 1Т0 + 1Т4, т.е. это сумма коэффициентов при самом младшем и самом старшем члене разложения.
III. Дальнейшее развитие представлений об эволюционной формализации у Д.В. Осадчего
После знакомства с интеллектуальными структурами Ж. Пиаже, Осадчий применил эволюционную "лестницу Пиаже" для анализа математических понятий в их генезисе, т.е. в их становлении. Такой анализ должен был показать естественное соотношение математических конструкций друг с другом и с уровнями развития человеческого интеллекта - со способами теоретического описания мира. Осадчий ввел следующие обозначения для уровней «лестницы Пиаже» [1]:
1). Уровень действия: это уровень дотеоретического восприятия мира - к нему относятся конкретные действия человека по упорядочению множества предметов вокруг себя. Например: счет.
2) Уровень понятия: это уже интериоризированное действие, освобожденное от конкретной природы объектов, которые упорядочивает человек. Это первая ступень абстракции, первая ступень теоретизирования. Пример: интериоризация действия "счет" дает понятие "число" (натуральные числа).
Важно отметить, что переход на каждый последующий уровень есть результат интериоризации, или, что то же самое, диалектического синтеза, который осуществляется в результате разрешения главного противоречия данного уровня развития. Так на первом уровне главное противоречие – это противоречие между ограниченностью возможностей действия и неограниченностью разнообразных объектов внешнего мира, на которые направлено это действие. Разрешается это противоречие в рождении абстрактного понятия, которое вбирает в себя все множество действий данного вида по отношению к внешнему миру.
Главное противоречие понятийного уровня – это противоречие между понятием и обратным к нему понятием. Обратимость – это то, что уничтожает исходное понятие. Разрешается это противоречие путем перехода на следующий уровень:
3). Уровень операции: здесь уже осуществляются операции над числами: вычитание, которое может обратить данное число в нуль; деление, которое может "уничтожить" число до единицы (путем деления на него же). На этом уровне уже существуют рациональные числа, отрицательные числа, может быть и иррациональные числа, порождаемые операцией извлечения корня (операцией, обратной возведению в степень); вероятно, к этому же уровню относится теория групп.
Главное противоречие этого уровня – это противоречие между операцией и границей ее применимости при решении какой-то задачи: противоречие это разрешается в формировании объектов следующего уровня – уровня структур, или операциями над операциями, или законов композиции операций. У Пиаже это называется формальными операциями.
4). Уровень структуры: "О структуре можно сказать, что это система тесно взаимосвязанных и взаимодействующих, скоординированных в одно целое операций". ?3, стр. 14?. И мы должны признать, что все известные нам математические структуры – теории аксиоматического типа (например: геометрия Евклида, формальная логика) – относятся к этому уровню развития.
Главное противоречие этого уровня – противоречие между неизменностью аксиоматических, формально-логических структур и беспредельной изменчивостью реального мира. Разрешение этого противоречия возможно лишь на следующей ступени развития, где реализуется процесс адаптации формальной логики к действительной посредством логики диалектической.
5). Уровень организации: Осадчий воспользовался термином Габриэля Крона, который сделал попытку построить математический аппарат для описания процессов развития, преобразования, эволюции объектов реального мира. "Эта организация реализуется введением групп преобразований, которые управляют развертыванием анализа, подобно тому как офицеры различного ранга направляют движение своих подчиненных" – писал о своем подходе Г. Крон [5, стр. 111].
Очевидно математический аппарат именно такого типа удовлетворил бы потребность естествоиспытателей, изучающих развивающиеся объекты, в языке теоретического описания этих объектов. Но на этом уровне также существуют противоречие – противоречие между адаптивностью, т.е. приспособительной активностью объекта, и внутренней активностью сложных объектов (под действием чисто внутренних побуждений), цели которых могут быть прямо противоположны друг другу. Противоречие между адаптивностью и инадаптивностью.
Для разрешения этого противоречия Осадчий ввел шестой уровень –
6). Уровень активности. Интересно, что уже после этого он познакомился с "лестницей Колберга", где также выделен аналогичный по смыслу шестой уровень. Никакие математические конструкции не достигают такой высоты.
Этот уровень последний, ибо активность иначе можно назвать полностью интериоризированным действием. На этом уровне спираль развития совершила полный оборот и активность является действием на новом витке раскручивания этой спирали. Т.е. мы можем назначить достигнутую на предыдущем витке спирали активность действием для следующего витка и, пройдя вновь все шесть ступеней "лестницы развития", получить полную интериоризацию уже этого нового действия в виде новой активности.
После оформления такой "лестницы развития", Осадчий пришел к выводу, что его алгоритм эволюционной формализации по существу описывает переход с одной ступени этой "лестницы" на последующую. Т.е. "лестница развития" шире по своим познавательным возможностям и конкретнее его прежней эволюционной формализации, и в дальнейшем он стал применять термин "эволюционная формализация" к приведенной выше "лестнице развития". Условимся называть ее в дальнейшем "лестницей эволюционной формализации".
В дальнейшем Осадчий поставил в соответствие каждой ступени этой лестницы образ определенного геометрического пространства (используя введенное им обозначение ТN), опираясь на то фундаментальное свойство "лестницы эволюционной формализации", что каждый последующий уровень относится к предыдущему как "содержимое" к своей границе. Другими словами, объекты соседних ступеней "лестницы эволюционной формализации" находятся в отношении вложения друг в друга.
Таблица 1.| Уровень эволюционной формализации | Геометрический образ | Симплекс | Обозначение абсолютного пространства |
| 1. Действие | Пустота | ° | T0 |
| 2. Понятие | Точка | · | T1 |
| 3. Операция | Прямая | — | T2 |
| 4. Структура | Плоскость | треугольник | T3 |
| 5. Организация | Объем | тетраэдр | T4 |
| 6. Активность | Гиперобъем | ? | T5 |
Осадчий предположил [1], что операция перехода с уровня на уровень формализуется в виде оператора интегрирования и дифференцирования. Операция дифферецирования имеет геометрический смысл взятия границы. Пример:
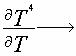 | 4Т3 | | тетраэдр Т4 |  | четыре треугольника 4Т3 |
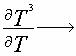 | 3Т2 | | треугольник Т3 |  | / — \ 3Т2 |
Операция, обратная дифференцированию – интегрирование осуществляет переход на следующий уровень:
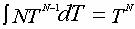 (1) (1)
число N под интегралом означает минимальное количество элементов (N-1) – го уровня, которые надо взять для образования границы достаточной величины, чтобы вместить "начинку" – один элемент следующего N – го уровня. Для наполнения границ надо иметь некоторый минимальный набор этих границ.
Поскольку, как мы указали выше, переход на каждый следующий уровень развития осуществляется путем диалектического синтеза, то операция интегрирования и является формализацией этого диалектического перехода, который описывается тремя известными законами диалектики. Обычно интегрирование понимается как некий аналог суммирования, т.е. в интегрировании осознан только переход количества в качество. Надо думать, что можно отождествить интегрирование и с другими законами диалектики, как с известными, так и с новыми, еще не сформулированными. Мы вернемся к этому вопросу в следующем параграфе. Сейчас же укажем на то, что переменная ТN в таблице 1 указывает лишь на величину размерности (мощности) пространства, соответствующего N – ой ступени развития объекта. Полностью пространство можно описать в виде суммы его границ, взятых с соответствующими коэффициентами (например: коэффициенты могут определяться биномиальным разложением для симплексов, т.е. для простейших объектов данной размерности). Вообще, пространством N – го порядка мы будем называть такую топологическую структуру, которая не содержит границы (гомологии) старше, чем ТN, независимо от количества младших, чем ТN границ (гомологий). Запись пространства в виде суммы его границ будем называть гомологической записью или гомологической структурой [1].
Приведем гомологическую запись для симплексов пространства разных уровней "лестницы эволюционной формализации":
Таблица 2.
| 1. Действие | 1 | | 2. Понятие | 1 + Т | | 3. Операция | 1 + 2Т + Т2 | | 4. Структура | 1 + 3Т + 3Т2 + Т3 | | 5. Организация | 1 + 4Т + 6Т2 + 4Т3 + Т4 |
| 6. Активность | 1 + 5Т + 10Т2 + 10Т3 + 5Т4 + Т5 |
Надо указать на одно важное свойство "лестницы эволюционной формализации" – самоподобность структур, её составляющих. Это свойство следует из того, что соотношение (1) выполняется независимо от значения N, и заключается в том, что независимо от того, что на какую ступень "лестницы" мы поместим изучаемый объект (а значит представим его различными гомологическими записями), мы будем осуществлять эволюционную формализацию объекта согласно соотношения (1). Это значит, что объекты разных ступеней вложены друг в друга подобным образом. Мы как бы можем видеть объект "при разном увеличении", с разной степенью подробности.
IV. Эволюционная формализация как дальнейшее развитие теории познания.
Диалектическая теория познания, в фундаменте которой лежат положения ленинской теории отражения (об активном, деятельном отражении мира субъектом; о процессе восхождения от абстрактного к конкретному в познании реальности; от знания неполного к знанию все более полному; о беспредельности движения познания "вглубь" объекта), получила дальнейшее развитие и конкретизацию в работах многих исследователей ХХ века, изучавших развивающиеся объекты различной природы. В поисках адекватного способа описания таких объектов исследователи неизбежно приходили к диалектическому методу изучения. В построениях операциональной теории интеллекта Пиаже, как и в "лестнице" морального развития Колберга, как и в "лестнице эволюционной формализации" Осадчего конкретизировался в виде определенных этапов процесс восхождения познающего субъекта ко все более полному знанию об объекте. И поскольку в основании этих построений лежит положение о том, что процесс познания есть интериоризированный (по терминологии Пиаже) процесс развития объектов реального мира, то восхождение познающего субъекта по "ступеням" "лестницы эволюционной формализации" обеспечивает ему построение системы описания, адекватной по своим выразительным возможностям изучаемому объекту, рассматриваемому на определенном этапе своего развития
В диалектике качественные переходы описываются тремя известными законами, каждый из которых фиксирует какую-нибудь одну сторону бытия развивающихся объектов: так, закон единства и борьбы противоположностей указывает на способ существования данного уровня развития; закон перехода количества в качество обращает внимание на способ осуществления перехода с одного уровня развития на другой; закон отрицания отрицания говорит о характере отношений между двумя последовательными переходами с уровня на уровень. Формализованное представление Осадчего о сущности качественных переходов между уровнями развития, выражаемое в виде интегрального преобразования (1), а также выделение шести конкретных уровней развития любого объекта реальности позволяет рассматривать известные законы диалектики как определенные способы осознания сущности качественного перехода, заключающейся в диалектическом синтезе, формализуемом операцией интегрирования. Эти же основания позволяют сделать предположение о возможности выделения и формулировки других законов диалектики, в форме которых будет осознан интегральный переход (1) на других ступенях "лестницы эволюционной формализации". Можно сказать, что существует единственный закон диалектики, выражаемый уравнением (1), но можно также сказать, что существует множество законов диалектики – столько, сколько существует уровней (ступеней) в «лестнице эволюции». Например: с этой точки зрения известная триада дарвинизма – "наследственность, изменчивость, отбор" – может рассматриваться как закон диалектики, описывающий переход со структурного уровня на уровень адаптирующейся организации; а известная ленинская формулировка революционной ситуации: "Верхи не могут управлять по старому, низы не желают жить по старому" – один из способов (в применении к конкретному объекту – обществу) выражения закона диалектики, определяющего сущность уровня активности или перехода уровня организации на уровень активности.
Конкретизация диалектического способа теоретизирования в "лестнице эволюционной формализации" является тем методом теоретического описания развивающихся объектов действительности, который позволит строить адекватные объектам теории на послеаксиоматическом – диалектическом уровне или, по нашей терминологии, на уровне организации. То есть сама "лестница эволюционной формализации" как способ описания находится на организационном уровне развития способов описания. Если средством описания на структурном уровне являются законы формальной логики, которыми можно описывать неразвивающиеся объекты, то средством описания на организационном уровне являются законы диалектического мышления, формализованные в виде "лестницы эволюционной формализации" Осадчего.
Чтобы привести пример описания посредством "лестницы эволюционной формализации", рассмотрим одно важное свойство самой "лестницы", которое и попытаемся выразить соответствующей "лестницей эволюционной формализации", построенной для этого свойства.
V. Законы сохранения – инварианты разных уровней развития.
Выделяя в процессе развития его конкретные этапы, мы подразумеваем определенную устойчивость, инвариантность этих этапов относительно каких-то преобразований. Другими словами, каждому уровню развития можно поставить в соответствие определенный закон сохранения (инвариант). Причем, связь между законами сохранения разных уровней должна выражаться преобразованием (1). Т.о. законы сохранения образуют "лестницу эволюционной формализации". Рассмотрим пример такой "лестницы" [1]:
1-й уровень: закон сохранения массы:
m = const.
2-й уровень: закон сохранения импульса:
mv = const.
Этот закон сохранения выражает первый закон Ньютона, его геометрическим образом будет последовательность отрезков равной длины и одного направления:
    
Рис. 2
т.е., геометрически это закон сохранения длины. Связь между приведенными
законами сохранения, записанная в виде интеграла (1), будет выглядеть так:
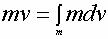
3-й уровень: Когда на тело массы m
начинает действовать другое тело силой гравитационного притяжения, первоначальная
траектория тела искривляется (т.е. импульс его уже не сохраняется) и оно
начинает двигаться по траектории, описываемой одним из конических сечений:
окружностью, эллипсом, параболой, гиперболой. Случай движения тела по эллипсоидальной
орбите рассмотрен И. Кеплером (2-й закон Кеплера): тело, движущееся в поле
тяготения другого тела по эллипсу, за равные промежутки времени заметает
равные по площади секторы (Рис. 3).
Рис. 3
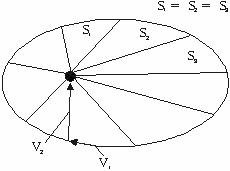
Т.е. это закон сохранения площади, который можно записать так:
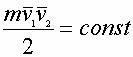 , ,
причем здесь 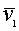 и и 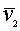
имеют различное направление. Интеграл, описывающий переход со второго уровня
на
третий дает нам привычную скалярную форму
этого закона сохранения:
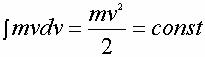 , ,
т.е. это закон сохранения энергии.
4-й уровень: Рассуждая по аналогии и введя
еще одну силу, действующую на данное тело m в ином направлении,
мы придем к выражению типа сохранения объема, т.е.:
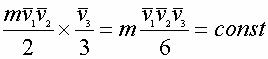
Интеграл, взятый для выражения для энергии, дает
нам этот закон сохранения в скалярной форме:
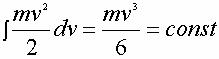
Такого типа соотношения, когда изменяются все три
сомножителя, а сохраняется их произведение, известны, например, в термодинамике
– уравнение Клапейрона для газов:
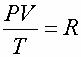 , ,
где P – давление , V – объем, T – температура, R – константа.
Рассматривая геометрические образы законов сохранения,
можно сделать важный вывод о соотношении законов сохранения соседних уровней,
а именно: когда перестает выполняться закон сохранения предыдущего уровня
(например, закон сохранения длины), начинает выполняться закон сохранения
следующего уровня (например, закон сохранения площади).
Согласно изложенному представлению можно записать
сохраняющиеся величины в механике в виде вложенных структур, которые можно
расположить на соответствующих ступенях "лестницы эволюционной формализации"
:
Так импульс 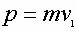 ; ;
Энергия 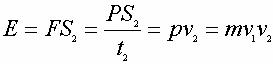 . .
"Физический смысл такой формулировки заключается
в том, что в пространстве скоростей (V1; V2; . .
.Vn) импульс и энергия имеют наглядные геометрические образы:
длину и площадь" [1].
На следующем уровне будет располагаться величина, имеющая размерность
(мощность х путь):
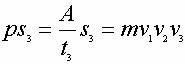
Распишем "лестницу эволюционной формализации" для
этих величин, введя обозначение: m = V0
Таблица 3.
| Уровень развития | Геометрический образ сохраняющейся величины | Механическая величина | Обозначение абсолютного пространства уровня |
| 1. Действие | | | T0 | | 2. Понятие | Номер точки | V0 масса | T1 |
| 3. Операция | Длина отрезка прямой | V0V1 импульс | T2 | | 4. Структура | Площадь поверхности | V0V1V2 энергия | T3 |
| 5. Организация | Объем тела | V0V1V2V3 мощность х путь | T4 |
Эта таблица напоминает таблицу законов сохранения,
предложенную Р.О. ди Бартини [14]. Он представил сохраняющиеся величины
в виде кинематической системы – произведения LnTn
, где L – длина, T – время, а n (...,-2,-1,0,1,2,...) – степень, в которой
берется соответствующая величина. Тогда скорость, например, будет записана
как L1T-1 , масса в этой системе записывается как
L3T-2 , импульс как L4T-3
, энергия как L5T-4, а последняя величина из
таблицы 3, которую ди Бартини называет «скорость передачи энергии», как
L6T-5. Эти величины, соответсвующие величинам, приведенным
в таблице 3, образуют главную диагональ таблицы ди Бартини. Можно сказать,
что «лестница эволюционной формализации» – это диагональ таблицы ди Бартини,
а таблица ди Бартини – это расширенный вариант лесницы эволюционной формализации.
А значит, если учесть все возможные переходы между клетками таблицы ди
Бартини, количество возможных законов диалектики, о которых мы говорили
в предыдущем параграфе, возрастает до бесконечности.
Наличие инвариантов (сохраняющихся величин) на каждом
из этапов развития наглядно представлено в гомологической записи пространства,
являющегося геометрическим образом данного уровня развития. В пространстве
N-го порядка старшая граница сохраняется, коэффициент при ней равен единице,
хотя для разных геометрических объектов N-й размерности число младших границ
может быть различным [1]. Так, кубу соответствует запись: 1 + 8Т1
+ 12Т2 + 6Т3 + 1Т4, а тетраэдру 1 + 4Т1
+ 6Т2 + 4Т3 + 1Т4. Для всех многогранников
коэффициент при Т равен единице. Это и есть образ сохраняющейся величины
организационного уровня развития, которому соответствует абсолютное пространство
Т4.
Инвариант данного уровня развития – это аксиоматика
этого уровня развития, т.е. основание для логического описания объекта,
достигшего этого уровня развития. Математический аппарат – это язык описания,
построенный, как и другие языки, с использованием определенной аксиоматики
(грамматики, синтаксиса). Здесь уместно привести два высказывания Д.В.
Осадчего [1]:
1. "О взаимности математики и познания: Каждому
уровню познания с одной стороны соответствует минимальный объект, а с другой
стороны – минимальный математический аппарат, который адекватно описывает
этот объект вплоть до возможности его (объект) синтезировать".
2. "О взаимности математики и развития: Математический
аппарат универсален не в силу своей якобы бессодержательности, а потому,
что описывает не конкретные свойства объектов, но этап эволюции, который
соответствует уровню развития самого материального объекта".
Так же, как на основании системы аксиом мы можем
вводить различные теоремы об объектах, подчиняющихся этим аксиомам, так
и система, описываемая абсолютным пространством N – порядка, имеет возможность
перераспределять свои младшие границы, порождая различные состояния объекта
N – уровня. Каждое состояние имеет структуру, отличающуюся коэффициентами
при младших границах в гомологической записи (как куб и тетраэдр, например).
Если разные состояния объекта данного уровня развития описываются суммами
младших границ с разными коэффициентами при членах, то имеется процесс,
протекающий на данном уровне развития [1]. Для описания процесса, протекающего
на данном уровне развития, необходимо ввести понятие энтропии.
VI. Энтропия – функция состояния данного уровня развития.
Фиксировать течение процесса можно по изменению коэффициентов
при разных границах, младших чем абсолютное пространство ТN.
Но мы условимся определять ход процесса по члену ТN-1 в гомологической
записи состояний.
«Если задано абсолютное пространство размерности
N, то плавающей метрической функцией состояния (энтропией) будет величина
пространства размерности (N - 1), вложенного в него» [1]. Т.е. каждому
уровню развития соответствует своя функция состояния – своя энтропия.
Энтропия – метрическая функция процесса или состояния, она является количественной
характеристикой системы. Система же в целом, т.е. качественно характеризуется
старшим членом гомологической записи ТN.
Наука изучает количественные закономерности процессов
различной природы. Эти закономерности фиксируются в форме различных принципов
оптимальности, например: принцип наименьшего действия Мопертюи в механике,
принципы Ле-Шателье в химии и физике, второй закон термодинамики, принципы
минимума производства энтропии Пригожина в неравновесной термодинамике,
различные принципы оптимальности в биологии [см. 6 и т.д.] – их можно вспомнить
еще много.
Все величины, подчиняющиеся перечисленным принципам
оптимальности из различных областей науки, являются энтропиями в
понимании Осадчего: "Любая наука о любом объекте, игнорируя старшую
границу пространства, характеризующего этот объект, строит науку об энтропии,
т.е. о мере младшей на порядок границы" [1]. Например, аналитическая
механика, созданная в XVIII веке, базируется на вариационном принципе –
приравнивании нулю вариации (производной) от некоторой величины (называемой
«действием»), которая качественно характеризует систему и является старшей
границей системы. Для выполнения этого требования другие величины, играющие
роль младших границ, должны удовлетворять некоторому соотношению, называемому
уравнением Эйлера – Лагранжа. Именно это уравнение и описывает динамику
системы во времени, т.е. является «наукой» о данной системе. В частности,
для консервативной системы (в которой выполняется закон сохранения энергии)
уравнениями Эйлера – Лагранжа являются уравнения Гамильтона.
Особенно наглядным это понимание энтропии является
в примере термодинамики "черных дыр", развиваемой С. Хоукингом [7], где
"черная дыра" как объект характеризуется массой, т.е. величиной, пропорциональной
объему, а энтропия "черной дыры" пропорциональна площади ее поверхности.
Т.е. качество объекта определяется величиной, выражаемой
абсолютным пространством Т4, а количественная характеристика
объекта определяется пространством на единицу меньшей размерности – Т3.
Для энтропии в статистической физике, определяемой
по формуле Больцмана:
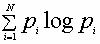 , ,
(где Pi – вероятность i – го состояния системы), оптимальность
протекания процессов, ею описываемых, заключается в том, что эти процессы
идут в направлении возрастания энтропии. Энтропия достигает максимума,
когда вероятности всех состояний равны между собой: P1 =
P2 = Pi = PN. Т.е. максимальной энтропии
соответствует наиболее симметричное распределение вероятностей. Можно сформулировать
и другие принципы оптимальности как принципы, требующие протекания соответствующих
процессов в направлении максимума симметрии того вида, который характеризуется
законом сохранения уровня развития, на котором рассматривается данный процесс.
Согласно теореме Э. Нетер, каждому закону сохранения можно поставить в
соответствие определенный вид симметрии, т.е. введенной нами в §V иерархии
законов сохранения можно поставить в соответствие иерархию видов симметрии.
Тогда интегральное преобразование (1), описывающее переходы между уровнями
развития, имеет еще один смысл – преобразования вида симметрии, что соответствует
преобразованию качества объекта, количественные же изменения – процессы,
протекающие на одном уровне развития – характеризуются энтропией или информацией,
понимаемой как "отрицательная энтропия" (Н. Винер) или "негэнтропия" (Л.
Бриллюэн).
VII. Следствия и примеры для естествоиспытателей.
Что может извлечь для себя из всего изложенного естествоиспытатель?
Во-первых, что существует способ формализованного
описания развивающихся объектов, по своей сущности адекватный таким объектам,
ибо эта формализация строится по тем же законам, по каким развивается объект
изучения. Это значит, что исчезает (или существенно уменьшается) произвол
в выборе разными исследователями, изучающими один и тот же эволюционирующий
объект, средств теоретического описания этого объекта – системы аксиом
для данного уровня изучения объекта и соответствующего ей математического
аппарата.
Во-вторых, что иные понятия и формализмы
принципиально неприменимы для адекватного развивающемуся объекту описания
этого процесса развития.
Например, широко известны попытки описать процесс
развития биологических объектов в терминах информации и энтропии [8]. Авторы
этих построений, констатируя недостаточность классического понимания количества
информации для такой задачи, вводят понятие "качества", "ценности" информации,
учет которого в виде некоего множителя даст якобы возможность описать процессы
качественного изменения, протекающие в биологических объектах, как информационные
процессы. Но, как мы старались показать, качественные переходы между уровнями
развития нельзя описать в рамках аксиоматики какого бы то ни было уровня
развития и соответствующего этому уровню развития математического аппарата.
Т.е. в данном примере: не домножение на удачно подобранный коэффициент,
а интегральное преобразование, проведенное над аксиоматикой (понятиями)
данного уровня, позволит описать качественный переход на следующий уровень
развития и получить аксиоматику, соответствующую этому новому уровню. Что
касается информации, то можно сказать что на каждом уровне развития существует
своя информация (как и своя энтропия) и сравнивать между собой эти информации
количественно бессмысленно.
В-третьих, что для математического описания
самого процесса развития объекта, а не только строения и функционирования
объекта на одном определенном уровне развития, недостаточно имеющихся математических
теорий аксиоматического типа. Нужен математический аппарат, адекватный
самой "лестнице эволюционной формализации", т.е. аппарат, принадлежащий
организационному уровню развития математики.
Таковым является "тензорный анализ сетей" Габриеля
Крона [5], где динамика или физика количественных процессов отделена от
качественного преобразования топологии пространств-сетей, в которых эта
динамика реализуется. Современная алгебраическая топология пришла к подобным
же конструкциям – это топосы Лаверра или пространства с переменной топологией
[15]. Сюда же относятся различные эвристические методы моделирования
развивающихся объектов: метод самоорганизации на основе многорядной селекции
(воплощение механизма дарвиновской эволюции в формальных структурах) А.Г.
Ивахненко и др. [9]; эвристический анализ информационных структур А.В.
Напалкова и Н.В. Целковой [10], суть которого состоит в описании процесса
синтеза абстрактных языков, работающих на конкретных уровнях переработки
информации мозгом, синтеза, который описывает переходы с уровня на уровень
в ходе переработки информации.
Метод эволюционной формализации позволяет увидеть
объект "стереоскопически", "объемно", как стопку фотографий, на каждой
из которых в рамках определенной аксиоматики описывается некое состояние
объекта – некий "срез" процесса его развития. Отдельные описания являются
дополнительными друг другу в том смысле термина «дополнительность», который
придал ему Нильс Бор: когда справедливо одно описание, тогда неприменимо
другое, и наоборот.
В качестве примера приведу анализ понятий и конструкций термодинамики,
проведенный Осадчим [1]:
Таблица 4.
| Уровень познания объектов термодинамики | Понятия и конструкции термодинамики | | 1. Действие | Координаты (q) и импульсы (p) частиц – область классической механики | | 2. Понятие | Температура – Т, объем – V, давление – Р, энтропия – S – как результат "интериоризации" в статистической физике микроскопических переменных (p,q) в макроскопические величины T, V, P, S |
| 3. Операция | Газовые законы, устанавливающие бинарные соотношения между полученными макроскопическими величинами (закон Бойля – Мариотта, Гей – Люсака) | | 4. Структура | Сюда относятся основные законы термодинамики – ее начала. Они создают ее структурную целостность. |
| 5. Организация | Только на этом уровне мы находим объекты неравновесной термодинамики, исследованные в работах И. Пригожина ?11?. Эти объекты (диссипативные структуры) уже надо рассматривать как развивающиеся (адаптирующиеся) объекты. | | 6. Активность | На этом уровне должна находиться термодинамика, которая изучает процессы в активных объектах, т.е. термодинамика живых существ. Можно сказать, что на этом уровне термодинамика переходит в биологию (или биофизику), т.е. назвав эту активность живого "действием" и выстроив над ним новую "лестницу эволюционной формализации", мы получим на разных ступенях этой "лестницы" разные известные нам свойства живых объектов. |
Казалось бы, разнесение понятий и конструкций термодинамики
по первым четырем ступеням очевидно и не требует какой-то специальной "эволюционной
формализации". Но выделение пятой и шестой ступеней уже неочевидно и позволяет
сделать нетривиальные выводы о понятиях этих уровней и операциях над этими
понятиями.
Рассмотрим ревербератор или спиральную автоволну
– простейшую диссипативную структуру, открытую в нелинейных химических
процессах. Если она принадлежит организационному уровню, то её существование
– это развитие, а развитие должно описываться интегральным преобразованием
(1). Уравнение логарифмической спирали:
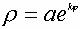 , ,
где k и а - константы.
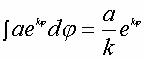 или или 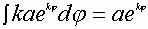
Обозначив 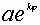 , стоящее под интегралом, через , стоящее под интегралом, через  i( i( ), a ), a 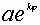 , стоящее после знака равенства, через , стоящее после знака равенства, через 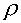 i+1( i+1(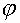 ), перепишем: ), перепишем:
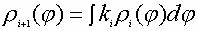
(2)
Выражение (2) аналогично выражению (1). Отличие состоит в том, что логарифмическая
спираль в результате применения интегрального преобразования (2) воспроизводит
себя без изменений (это ее свойство), в то время как в выражении (1) результат
интегрирования явно отличается по степени своей сложности от выражения,
стоящего под интегралом. Поэтому совсем неочевидно, что поведение ревербератора
должно описываться формулой (2), но если мы отнесли его как объект к уровню
организации, то именно такое описание объекта будет адекватно самому объекту.
Можно предложить более общий вид выражения (1):
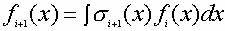
(3)
где .jpg) – функция, описывающая состояние объекта на i - м уровне его развития; – функция, описывающая состояние объекта на i - м уровне его развития; 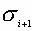 – некоторая функция распределения, определяющая состояние системы на (i + 1) уровне. В формулах (1) и (2) эта функция распределения равна просто постоянной n в (1) и k в (2). – некоторая функция распределения, определяющая состояние системы на (i + 1) уровне. В формулах (1) и (2) эта функция распределения равна просто постоянной n в (1) и k в (2).
Последнее обстоятельство говорит о том, что
в этих двух случаях мы рассматриваем процесс развития, протекающий в неизменной
среде.
В более общем случае (3) среда будет оказывать влияние
на результат процесса развития путем изменения функции распределения sigmai(x).
Для спиральной автоволны это означает, что в неоднородной среде она будет
изменяться каким-то особым образом, зависящим уже от вида переменной k(fi)
в выражении (2), что в действительности и наблюдается – в неоднородной
среде автоволна быстро вырождается в хаотическое движение.
Выражение (3) является по сути дела уравнением,
описывающим соотношение между микроскопической функцией b(q, p, x, t) и
макроскопической функцией B(x, t) в статистической механике [12]:
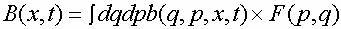
(4)
где .jpg) – функция распределения, означающая плотность вероятности нахождения системы в точке (p,q) фазового пространства. Таким образом, можно сказать, что выделение в статической механике двух состояний: микроскопического и макроскопического, связанных выражением (4), является частным, вырожденным случаем "лестницы эволюционной формализации", когда число её ступеней сводится до двух первых (именно таким образом в таблице 4 связаны понятия первого и второго уровней). – функция распределения, означающая плотность вероятности нахождения системы в точке (p,q) фазового пространства. Таким образом, можно сказать, что выделение в статической механике двух состояний: микроскопического и макроскопического, связанных выражением (4), является частным, вырожденным случаем "лестницы эволюционной формализации", когда число её ступеней сводится до двух первых (именно таким образом в таблице 4 связаны понятия первого и второго уровней).
В полной "лестнице эволюционной формализации" мы
для каждого уровня будем иметь свое микроскопическое и свое
макроскопическое состояния, связанные выражением (3) , т.е. макросостояния
данного уровня будут микросостояниями для последующего уровня развития.
Это обстоятельство объясняет, почему для описания развивающихся объектов
(в частности живых) неприменимы понятия энтропии и информации, взятые из
статистической физики, о чем мы говорили выше, – для каждого уровня развития
энтропия (и информация) должна определяться особо в соответствии
с физическим представлением о том, что энтропия это логарифм числа микросостояний,
которыми может быть реализовано данное макросостояние, но дополненным
представлением Осадчего об относительности понятий "микро" и "макро"
в развивающемся объекте. Именно поэтому попытка подсчитать энтропию биологического
объекта (энтропию, определяемую как в статистической физике, где выделяются
только два уровня) приводит к абсурдным выводам о том, что энтропия человека
и энтропия камня того же веса не отличаются друг от друга [13].
На шестом уровне развития термодинамики (табл. 4)
мы выходим в область биологии. Рассмотрим пример применения "лестницы эволюционной
формализации" для анализа биологических объектов:
Таблица 5.
| Уровень развития | Биологическое явление |
| 1. Действие | Химический катализ: | | 2. Понятие | Фермент как субъект, интериоризировавший каталитическое действие: | | 3. Операция | Цепочка ферментов, осуществляющих общую биохимическую реакцию, в которой ферменты связаны отношениями активации – ингибирования (например, ферменты гликолиза) | | 4. Структура | Мембранная структура, объединяющая все ферменты, выполняющие определенную биологическую функцию, например: ферменты окислительного фосфоримироваиня в структуре митохондрии. |
| 5. Организация | Адекватные изменения состояния системы ферментов и матрицы, в которой они закреплены (мембраны), в соответствии с изменением условий среды. Здесь уже появляется в поле зрения наследственная структура биосинтеза ДНК -> РНК -> белок, обеспечивающая эту адаптацию (эта структура, рассматриваемая статически, есть объект Т4 в нашей теоретической "лестнице"). Пример: органелла, взятая в целом, вместе со своим наследственным аппаратом: митохондрия, хлоропласт, ядро клетки. |
| 6. Активность | Клетка в целом, рассматриваемая как активная "питающаяся" структура. Питается она по своим внутренним причинам (голод, понятный только тому, кто голодает). |
На примере этой "лестницы" видно, что "активность"
есть возвращение к "действию" на новом витке спирали развития. Ведь химический
катализ аналогичен процессу питания: продукты питания (субстрат) превращаются
в отходы (продукт) при помощи клетки (катализатора). Точно так же в таблице
4 "действие" – механический импульс аналогичен "активности" – импульсу
активности живого существа (перемещению его, но по его внутреннему побуждению
в отличие от механического импульса неживой частицы).
На два важных свойства "эволюционной формализации"
необходимо указать:
1). Подобно тому, как от каталитического
акта путем восхождения по "лестнице эволюционной формализации" мы пришли
к клетке, так и от многих других элементарных "действий", лежащих в основе
жизнедеятельности клетки, мы можем прийти путем "эволюционной формализации"
к соответствующим (аналогичным этим "действиям") "активностям" клетки.
Например: от "действия" – матричной редупликации макромолекул – мы можем
прийти к делению клетки на уровне "активности". Это тоже клетка, но здесь
в понимании её исследователем фиксируются иные её свойства, чем в
табл. 5. "Что посеешь – то пожнешь". Таким образом, мы можем для одного
объекта (клетки) построить много "лестниц эволюционной формализации", в
которых он будет занимать один и тот же уровень развития (в нашем случае
– уровень "активности"). Все эти построения будут дополнительны друг к
другу в смысле дополнительности Бора, т.е. мы сможем понять объект таким,
каков он есть, только проведя множество параллельных " эволюционных формализаций"
для этого объекта, каждая из которых откроет перед нами какую-то одну его
сторону (сторону его "активности", в нашем случае).
2). Но кроме этой "параллельной" дополнительности
есть еще один вид дополнительности, который мы назовем "последовательной".
Суть его состоит в том, что один и тот же объект (клетка) может располагаться
на разных ступенях "лестницы эволюционной формализации" в зависимости от
того, эволюционную формализацию какого объекта (взятого в качестве "действия")
мы проводим. Например, если в качестве "действия" взять питание клетки,
то после проведения эволюционной формализации на уровне активности мы получим
деятельность организма по осуществлению своего питания. Но в другом случае
(если в качестве "действия" выбрать другие акты жизнедеятельности разной
степени сложности) клетка как таковая может находиться и на уровне
структуры (тогда уровень организации будет занимать ткань, а уровень активности
– орган), и на уровне операции (тогда уровень структуры будет занимать
ткань, уровень организации – орган, а уровень активности – система органов),
и на других уровнях. И описания одного и того же объекта в рамках разных
уровней его рассмотрения в различных "лестницах эволюционной формализации"
дополнительны друг к другу в смысле дополнительности Бора. Это и есть "последовательная"
дополнительность – дополнительность в рассмотрении одного и того же объекта
на разных ступенях "лестницы эволюционной формализации". Полное представление
о развивающемся объекте можно получить, лишь имея его "параллельные" и
"последовательные" дополнительные описания. А точнее, при анализе объектов
организационного уровня и создания их теоретических описаний, мы будем
получать множество относительных описаний, каждое из которых представляет
собой проекцию изучаемого объекта на подход конкретного исследователя к
этому объекту, его методологическую установку. Таким образом мы утверждаем,
что субъективность рассмотрения объекта объективно присуща самому
нашему способу познания (эта точка зрения со времени создания теории относительности
Эйнштейна все более завоевывает себе признание в различных областях науки).
Но, в отличие от полной субъективности в аксиоматическом способе построения
теории для развивающегося объекта, которая критиковалась нами в §1, мы
утверждаем субъективность теоретического описания, "организованную" в соответствии
с закономерностями самого процесса развития, отражаемыми в "лестнице эволюционной
формализации".
* * *
Во всех областях современной науки на передний план выходят проблемы
развития, эволюции: в космологии, в биологии, в экологии, в химиии всвязи
с колебательными химическими реакциями, в физике всвязи с изучением самоорганизации.
Мы старались показать в этом очерке, что развивающиеся объеты принадлежат
организационному уровню познания и только на этом уровне могут быть адекватно
поняты и теоретически описаны. «Эволюционная формализация» Осадчего – это
и есть способ теоретизирования на организационном уровне.
Литература:
1. Конспекты лекций Д.В.Осадчего за 1983-1984 гг.
2. Б.М.Медников. Аксиомы биологии. М.1982.
3. И.З.Цехмистро. Поиски квантовой концепции физических оснований сознания.Харьков.1981.
4. Знание-Сила,1983,№11, с.39.
5. Г.Крон. Тензорный анализ сетей.М.1978.
6. Р.Розен. Принцип оптимальности в биологии.М.1969.
7. Д.А.Киржниц, В.П.Фролов. Черные дыры, термодинамика, информация.
– Природа, 1981,№11,с.2.
8. И.И.Шмальгаузен. Кибернетические вопросы биологии. Н-ск.1968.
9. А.Г.Ивахненко, Ю.П.Зайченко, В.Д.Димитров. Принятие решений на основе
самоорганизации.М.1976.
10. А.В.Напалков, Н.В.Целкова, И.Ф.Моисеев. Эвристический анализ информационных
структур.М.1975.
11. Г.Николис, И.Пригожин. Самоорганизация в неравновесных системах.М.1979.
12. Р.Балеску. Равновесная и неравновесная статистическая механика.
т.1. М.1978, с.52-53.
13. Л.А.Блюменфельд. Проблемы биологической физики.М.1977,с.27.
14. П.Г.Кузнецов. Искусственный интеллект и разум человеческой популяции.
– Приложение к кн.:Е.А.Александров. Основы теории эвристических решений.М.1975.,с.212.
15. И.А.Акчурин. Единство естественнонаучного знания. М.1974.
ДОПОЛНИТЕЛЬНЫЕ ЗАМЕЧАНИЯ О МЕТОДЕ ЭВОЛЮЦИОННОЙ ФОРМАЛИЗАЦИИ
(ноябрь 1985)
Оглавление.
VIII О типах научного знания.
IX Типы научного знания в
связи со схемой Н.А.Бернштейна.
X Три принципа познания
ХХ века.
XI Каким образом разные типы
знания входят в культуру?
XII Что такое теоретическая биология?
XIII Как изменяется педагогическая задача при
переходе со структурного уровня на организационный.
Литература
VIII. О типах научного знания.
Разным ступеням лестницы эволюционной формализации
(которую мы в дальнейшем будем называть «лестницей Пиаже») будут соответствовать
различные типы научного знания. Так, структурному уровню соответствует
аксиоматико – дедуктивный тип научных теорий, идеалом которого является
геометрия Евклида и механика Ньютона. Научное знание предыдущих ступеней
лестницы Пиаже представляет собой частные случаи этого типа знания. Аксиоматико
– дедуктивная теория – это не что иное, как язык описания (таков синтаксис
обычного человеческого языка, таково же строение математических описаний
- теорий). Поэтому, наука, соответствующая этому типу знаний – это описательная
наука. Её задача – составление полезных (для данного общества) описаний
реальности. Идеал такой науки сложился в XVII веке трудами Декарта, Бекона,
Галилея, Ньютона: именно с этого времени истинное знание понимается как
полезное в производственной практике знание, с этого времени практика считается
критерием истины, а знание, подтвержденное практикой, считается объективным.
Это значит, что в рамках аксиоматико – дедуктивной теории качество субъекта
познания не принимается во внимание (это качество однозначно зафиксировано
в аксиомах теории). Т.е. на самом деле объективность существует только
в рамках выбранной аксиоматики (парадигмы), а значит, эта "объективность"
субъективна, т.е. зависит от качества субъекта познания (парадигмы культуры,
которая его задает). Субъект познания, как считал Кант, несет в себе априорное
знание о пространстве и времени, в которые он и втискивает изучаемые объеты.
Условно можно изобразить этот тип познания в виде
схемы:
С => О,
где С – субъект, О – объект. Это монологическое знание (термин М.М.Бахтина
[19]: субъект произносит монолог об объекте, при этом объект безмолвствует,
поэтому и является объектом. Субъект своим монологом опредмечивает объект.
Организационному уровню лестницы Пиаже соответствует
тип знания, который выражается самой лестницей Пиаже, её логикой: на каждой
ступени лестницы Пиаже мы строим описание аксиоматико – дедуктивного типа,
которое включает в систему своих аксиом характеристику познавательной позиции
исследователя (качество субъекта); при переходе на новую ступень по лестнице
Пиаже в процессе познания объекта мы изменяем, трансформируем свою познавательную
установку, свое видение объекта исследования (изменяется качество субъекта),
что выражается в переходе к новой системе аксиом на новой ступени лестницы
Пиаже.
Изучая развивающиеся объекты, исследователь вынужден
самой логикой своего предмета изучения обращаться к вопросам теории познания
(Бор, Эйнштейн, Пригожин, Мейен, Чайковский), поэтому этот тип научного
познания можно назвать знанием гносеологического типа. Этот тип познания
можно изобразить в виде схемы:
С2 <=>О2(С1 => О1)
где С2 – субъект, О2 – объект, т.е. сам объект является познающим субъектом
(С1), или, что то же самое, развивающимся, адаптирующимся к своей среде
обитания О1 объектом.
Знание этого типа уже явно субъективно (субъект
С2 видит объект О1 субъективно – "глазами" субъекта С1). Кроме того, субъект
С1 реагирует на когнитивные действия субъекта С2, т.е. вступает с
последним в диалогическое общение (встречные стрелки на схеме). Это диалогическое
знание по М.М.Бахтину [19]( знание типа «Я<=>ТЫ» по Мартину Буберу или
знание типа «Я<=>Я» по Ю.М.Лотману [15]).
Лестница Пиаже – это и есть алгоритм трансформации
познавательной упаковки исследователя (парадигмы) при познании развивающегося
объекта. Сама лестница Пиаже принадлежит организационному уровню познания.
Уровню активности соответствует познавательная ситуация,
когда субъект прекращает адаптивный процесс "следования за объектом познания"
по ступеням лестницы Пиаже и отождествляет себя с объектом исследования
в акте "интуитивного усмотрения истины". Именно это происходит в процессе
художественного творчества, в искусстве и в акте установления нового закона
в науке [8].
Субъект, отождествляясь с объектом, начинает "жить
жизнью этого объекта", "чувствовать чувствами этого объекта". Очень четко
этот способ познания выражен в дзен-буддизме, в учении йоги (самадхи-йога).
Условно этот тип познания можно выразить схемой:
С <= О которая эквивалентна схеме: о <= С
Здесь субъект познания умаляет свою активность настолько, что его собственная
субъективность как бы затухает и он становится местом, где в полную меру
проявляется субъективность познаваемого объекта (субъекта). Используя церковную
терминологию, можно сказать, что сущность этой познавательной позиции заключается
в аскезе. Знание уровня активности можно назвать знанием этического типа,
ибо отождествление с изучаемым объектом возможно только при наличии у субъекта
этического отношения любви, сочувствия к объекту. Примером подобной
познавательной позиции в науке является философский "принцип дополнительности"
Бора (ибо он предполагает сочувственное отношение друг к другу дополнительных
точек зрения на объект), "принцип сочувствия" Любищева – Мейена [4]. Необходимость
такого принципа в познании человека хорошо показана у Л.Н. Толстого [5].
IX. Типы научного знания в связи со схемой Н.А. Бернштейна.
Н.А.Бернштейн [1] предложил выделить в математике
следующие конструкты:
1). Номинаторы: числа, векторы, тензоры, точки,
отрезки и т.д.
2). Операторы: +, –, :, х, "корень"
и т.д.
3). Алгоритмы 1-го рода: правила вычислений, выражаемые
в виде формул (например, правило нахождения корней уравнения 2-й степени).
4). Алгоритмы 2-го рода: правила вычислений, невыразимые
в виде формул.
Нетрудно увидеть в переходе от алгоритмов
1-го рода к алгоритмам 2-го рода реализацию ограничений, накладываемых
на возможности научного описания теоремой Гёделя "о неполноте описания"[2]:
«из любой системы аксиом невозможно вывести дедуктивно все свойства даже
самого простого (например, натуральный ряд чисел) объекта – всегда найдутся
свойства, для вывода которых понадобится ввести дополнительные аксиомы,
расширить выразительные свойства языка описания». Следствием этой теоремы
является существование функций, которые можно вычислить, но нельзя однозначно
записать на каком-либо языке описания. Единственный способ представления
этих функций – это сам алгоритм вычисления в процессе его реализации.
Еще ярче свойство подобных функций выглядит
в формулировке Дж. фон Неймана, который показал, что сложную систему иногда
можно создать, но нельзя описать (т.е. для воспроизведения такой системы
на ЭВМ требуется программа бесконечной длины).
Поскольку конструкция Бернштейна, как нетрудно видеть,
однозначно соответствует ступеням лестницы Пиаже со второй по пятую, то
нам становится понятной особенность знания организационного уровня (которому
соответствует алгоритм 2-го рода Бернштейна) – его выразимость только посредством
алгоритма, каковым и является сама лестница Пиаже. Т.е. мы видим, как при
переходе от структурного уровня познания к организационному, знание из
описания превращается в алгоритмическую деятельность
(вычисление). Свою полную реализацию эта тенденция перехода от описания
к деятельности находит на уровне активности, где знание является
нам в форме этической деятельности.
Рассмотренная тенденция поясняет необходимость всё
большего учета качества субъекта познания (всё большей субъективности знания)
при движении от структурного уровня к уровню активности. Становится также
ясно, что "объективное" знание возможно только как знание описательного
типа на структурном уровне. По аналогии с определениями типов знания на
рассмотренных выше уровнях, знание структурного уровня назовем знанием
онтологического типа (в отличие от знания гносеологического и этического
типов).
Как обнаруживают себя объекты организационного уровня
в попытках описания их средствами структурного уровня?
1). Переход от детерминированного к вероятностному
описанию (именно таким образом наука впервые столкнулась с объектами организационного
уровня в термодинамике Больцмана и затем в квантовой механике).
2). Появление в формулах, описывающих эти объекты,
иррациональных величин "пи", е и т.д., которые являются образом
несоизмеримости того пространства, в котором существуют развивающиеся объекты,
с тем пространством логического описания, в котором мы пытаемся понять
эти объекты [11].
3). Другим образом несоизмеримости является обнаружение
бесконечностей (расходимостей) при попытках структурного описания процессов
развития (физика элементарных частиц).
Можно сказать, что сама жизнь, которую мы понимаем
как процесс адаптации, является средством, способом, алгоритмом,
посредством которого живое преодолевает несоизмеримость себя с неживой
средой обитания. Станислав Лем назвал такое «знание посредством тела» технологией
[20].
Следствие: в формуле для интегрального преобразования
Осадчего для сложных развивающихся объектов в качестве весовой функции
будет писутствовать иррациональное выражение – экспонента, как в преобразовании
Фурье или Лапласа, или же, расписывая экспоненту в виде степенного ряда
(см. формулу ниже), мы получим вместо одного интегрального преобразования
бесконечный ряд интегралов типа ряда Винера или ряда Вольтерра [16].
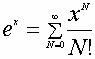
X. Три принципа познания ХХ века.
1). Принцип неполноты описания К. Геделя [2]:
этот принцип обосновывает переход от структурного уровня познания к организационному
и, тем самым, обосновывает необходимость движения исследователя по ступеням
лестницы Пиаже.
2). Принцип Э. Нетер: "каждому закону сохранения
отвечает определенный принцип симметрии и наоборот" – т.е. до тех пор,
пока мы видим, что некий принцип симметрии изучаемого объекта выполняется
при функционировании этого объекта, мы находимся в пределах одной ступени
лестницы Пиаже и наблюдаем именно функционирование, а не процесс развития
объекта. Когда происходит нарушение симметрии (например, ?-распад в физике)
– это является сигналом того, что перед нами совершается процесс развития
– переход на новую ступень лестницы Пиаже.
3) Принцип дополнительности Бора [3]: мы
строим лестницы Пиаже для одного и того же объекта, назначая "действиям"
разные виды активности для разных лестниц Пиаже. Истинное знание об объекте
заключается в дополнительности этих лестниц Пиаже – это есть максимально
возможное приближение к истине на организационном уровне познания.
Только на уровне активности, и только интуитивно
[8] возможен синтез этих дополнительных конструкций (если исследователь
занимает этическую позицию, выражаемую "принципом сочувствия") – таким
образом мы переходим к изучению нового объекта, качественно новой активности
этого объекта, которую мы подаем на вход новой лестницы Пиаже в качестве
действия.
* * *
Все три типа познания, о которых шла речь выше, присутствуют
в любой культуре. Соотношение между ними такое: новая идея рождается внелогически,
интуитивно [8], на активностном уровне познания (этому уровню соответствует
в культуре – поэзия), затем эта идея ассимилируется на организационном
уровне познания, который представлен в культуре философией, и лишь в дальнейшем
эту идею включает в систему своих аксиом наука структурного уровня. Примером
такого движения новой идеи является движение идеи развития в новоевропейской
культуре: эта идея появилась в поэзии Шекспира в XVII веке, затем была
осознана в философии конца XVIII века (Гете, Гегель), и с середины XIX
века до нашего времени эта идея активно внедряется в естествознание (Дарвин,
Больцман, Пригожин) [13].
XI. Каким образом разные типы знания входят в культуру?
Культура, или культурная компонента хозяйственно-культурного
типа (ХКТ) обязательно включает в себя иррациональную часть. Рациональное
– это то, что выразимо логически, средствами языка (описательная наука,
право и т.п.). Иррациональное – это то, что вербально невыразимо: религия,
искусство, обычаи, этика.
Каждой культуре соответствует своя наука, т.е. своя
рациональная компонента, поэтому научные представления средневекового Китая,
например, нельзя понять в терминах европейской науки того же времени. Наука
Древней Греции (в лице Аристотеля) неинтерпретируема в понятиях науки эпохи
Возрождения (Леонардо да Винчи), которая, в свою очередь, непонятна в рамках
парадигмы науки Нового времени (Ньютон, Бекон).
Мы уже говорили выше, что в XVII веке сформировалась
описательная наука структурного уровня познания, в рамках которой многие
исследователи, по своему культурному облику выходящие за пределы новоевропейской
традиции, не были понятны научным сообществом (Гете, Окен, Лейбниц).
С начала ХХ века мы переживаем процесс трансформации
европейской культуры, который выражается в рациональной сфере в изменении
объекта и выразительных средств науки. Наука всё больше обращается к изучению
объектов организационного уровня (космология, биология, синергетика, социология)
и пытается описать сам процесс развития, т.е. наука прорывается на организационный
уровень познания, на котором безраздельно господствовала философия в европейской
культуре Нового времени.
Эта тенденция выражается в изменении способа описания
объектов исследования: переход от детерминированного описания аксиоматико
– дедуктивного типа к вероятностному описанию, к неформализуемым алгоритмам,
что особенно ярко видно на примере поиска решения проблемы искусственного
интеллекта, изучения сложных задач в режиме диалога "человек – машина".
Эта тенденция выражается в обращении естествознания
к гносеологическим проблемам в конкретных областях исследования каждой
науки. В итоге происходит экспансия рациональной части культуры
(науки) на область иррациональной части культуры, что выражается в гуманитаризации
естествознания, заключающейся во включении в ткань науки качества самого
субъекта познания. Т.е. при движении от науки структурного типа к науке
организационного типа происходит распространение методов познания искусства,
религии на науку ("для приближения к истине необходимо бесконечное количество
актов веры" – формулировка теоремы Гёделя, принадлежащая Феферману). Эта
тенденция найдет своё полное выражение при переходе нашего познания
на уровень активности, где происходит полное слияние рационального и иррационального
компонентов культуры (к этому относится известная фраза К. Маркса о слиянии
в науке будущего естествознания с гуманитарными науками) (Циолковский,
Тейяр де Шарден) [6,7].
Вывод: культура новоевропейского времени
(и наука этого времени) занимает период с начала XVII века до 70х годов
ХХ века. С 70х годов ХХ века мы входим в иной тип культуры,
который характеризуется иным сочетанием рационального и иррационального
(естественнонаучного и гуманитарного знания) – наука переходит на организационный
уровень познания [12].
Описательная наука (структурный уровень) относится
к иррациональным компонентам культуры (организационный уровень и выше)
как поверхность относится к ограничиваемому ею объему. И так же, как нельзя
себе представить объема без ограничивающей его поверхности, так нельзя
оторвать научные представления данной культуры от религии, этики, искусства
этой культуры.
Однако в рамках традиций новоевропейской науки
новая идея оценивается только исходя из рациональных критериев, что часто
препятствует её принятию обществом, хотя, как говорилось выше, новое рождается
именно в иррациональной сфере (внелогически) на уровне активности.
Сказанное относительно культуры верно и в отношении
психологии познания отдельного человека. Его мышление состоит из рационального
сознания и иррационального подсознания (сверхсознания – З. Фрейд). Именно
в сфере подсознания происходит генерация нового посредством интуиции, а
затем это новое интерпретируется в сознании логическими конструкциями.
Следствие: неразрывность рационального и
иррационального в культуре и мышлении приводит к тому, что примитивное
состояние иррационального (в человеке: художественный вкус, эстетические
принципы; в культуре: религия, искусство) неизбежно сопровождается примитивным
состоянием рационального (научного знания о мире, логических средств описания
этого мира).
XII. Что такое теоретическая биология?
В биологии часть знания построена по типу описательного
аксиоматико-дедуктивного знания современной физики – это конструктивные
описания различных блоков и систем, из которых построено живое. К этому
типу знания относятся молекулярная биофизика, молекулярная генетика и генная
инженерия, биохимия, физиология систем органов, популяционная генетика,
экология. Все эти науки можно назвать различными «биофизиками», т.е. физическими
описаниями различных уровней изучения живого.
Но в биологии есть ряд основных проблем, которые
неописуемы в рамках аксиоматико-дедуктивного способа. Сюда относятся все
проблемы, связанные с развитием, с качественным преобразованием живого
объекта: онтогенез, геронтогенез, развитие патологий, онкогенез, филогенез,
эволюция биосферы и т.п. Здесь живой объект является объектом организационного
уровня и может быть познан только средствами организационного же уровня,
каковым является теория (и алгоритм) познания лестницы Пиаже. Таким образом
для адекватного понимания биологического объекта необходимо иметь теорию
как минимум организационного уровня. Значит, теоретическая биология есть
реализация лестницы Пиаже для биологически проблем, т.е. это наука гносеологического
типа [17].
Ю.Одум изобразил эту специфику биологической науки
в виде слоеного пирога, горизонтальные разрезы которого (слои) соответствуют
тем наукам, которые мы назвали «биофизиками», а вертикальные соответствуют
организационным проблемам биологии. Причем именно вертикальные сечения
организуют слои в иерархии, которые мы называем лестницами Пиаже. Набор
вертикальных сечений («кусков пирога») представляет собой дополнительные
друг дуругу (в смысле нашей «параллельной дополнительности») лестницы Пиаже
[21].
XIII. Как изменяется педагогическая задача при переходе со структурного
уровня на организационный.
Знание структурного уровня заключается: 1) в системе
аксиом; 2) в логике дедуктивного вывода. Следовательно педагогическая задача
на этом уровне заключается в запоминании данного набора аксиом и основных
правил логического вывода. Нетрудно видеть, что знание такого типа безразлично
к качеству субъекта – в этом состоит объективность знаний, т.е. педагога
не интересуют особенности ученика. Вернее, эти особенности понимаются чисто
количественно: "более способный – менее способный", исходя из затраты времени
на усвоение учеником данной системы знания.
Знание организационного уровня, как мы говорили,
явно включает в себя качество субъекта познания, поэтому и педагогическая
задача будет заключаться не в том, чтобы выучить основные положения теории
познания лестницы Пиаже, а в том, чтобы провести данного ученика
по ступеням лестницы Пиаже на примере разных задач, результатом чего должно
быть приобретение учеником того способа видения окружающего мира, который
выражается в идеологии лестницы Пиаже. Т.е., если на структурном уровне
педагогическая задача – это накопление знания, то на организационном уровне
– это формирование субъекта познания. Таков путь познания в школе
"дзэн", в учении даосизма (Дао – это путь и обучение здесь – это следование
определенному пути; цель обучения заключается не в финале пути, – сам путь,
сама деятельность субъекта в пути – вот цель в учении "дао") [18].
* * *
Так, с неожиданной стороны нашему взору открылся
путь слияния считавшихся до сих пор различными, и даже чуждыми друг другу
областей культуры (как внутри одной культуры, так и разных культур, принадлежащих
к различным типам соотношения рациональной и иррациональной компонент).
Сама логика движения человеческого познания приводит нас к необходимости
трансформации способа познания и самого понимания того, что именно, какую
деятельность считать познанием.
В нашем рассмотрении стало очевидным, что великие
этические учения разных эпох и народов (учения Лао-Цзы, Христа, Будды,
Л.Н. Толстого и др.) не лежат в стороне от главного пути движения человеческого
познания, а представляют собой достижения познания на уровне активности,
в то время, как рациональные формы знания (научное знание в собственном
смысле слова) – это достижения познания на уровне структурного знания (а
в этом веке научное знание распространяется и на организационный уровень
познания при попытках описания развивающихся объектов, вторгаясь в область,
традиционно попадавшую в европейской культуре Нового времени под юрисдикцию
философии). Процесс слияния "двух культур" [14] позволяет нам увидеть,
осознать и рационально сформулировать то понимание цели для человечества
(понимаемого как часть природы, способная к познанию), которую интуитивно
понимали основатели мировых религий, и которую наиболее четко сформулировал
в нашем веке Тейяр де Шарден [7].
Литература:
1. Н.А.Бернштейн. Предисловие к книге – Черныш, Напалков. Математический
аппарат биологической кибернетики.М.1964.
2. Манин. Теорема Геделя – Природа,1975,№12.
3. Фейгенберг. Принцип дополнительности в описании психических явлений
– Природа,1985,№2
4. С.В.Мейен. Принцип сочувствия – Пути в незнаемое.М.1977.
5. Л.Н.Толстой. О жизни. – собр.соч. т.17,1984.
6. А.Л. Чижевский. О Циолковском – Химия и жизнь, 1977,№1
7. П.Тейяр де Шарден. Феномен человека.М.1965
8. Фейнберг. Кибернетика, логика, искусство.М. 1981.
9. А.А. Любищев. Уроки самостоятельного мышления – Изобретатель и рационализатор,
1975, №8,9.
10. Абелев. Этика: цемент науки – Химия и жизнь, 1985,№2
11. Ю.В. Чайковский. О случайности вообще и о случайных мутациях –
Химия и жизнь, 1977, №9.
12. И. Пригожин. От существующего к возникающему. М.1985.
13. Г. Волков. Сова Минервы. М.1985.
14. Ч. Сноу. Две культуры. М. 1973.
15. Ю.М. Лотман. О двух моделях коммуникации в системе культуры. –
Труды по знаковым системам, вып.6, Тарту, 1973, с.227.
16. Н. Винер. Кибернетика. Дополнительные главы. Глава Х. М.1968.
17. Ф.И. Гиренок. Теоретическая биология и физическая картина мира.
– Биология и медицина. М. 1985.
18. Пронников, Ладанов. Японцы. М.1985.
19. М.М. Бахтин. Эстетика словесного творчества. М.1979.
20. С. Лем. Сумма технологий. М. 1968.
21. Ю. Одум. Основы экологии. М. 1975. |

