|
|
Количество статьи: 297
Статьи за 24 часа: 0
[ Все статьи | Поиск | Top 10 | Категории ]
Морфология законов природы
В начале XVIII века Пьер де Мопертьюи обратил внимание на то, что законы Ньютона допускают вариационную трактовку. Он показал, что движение, совершающееся согласно законам Ньютона, требует минимизации некоторого функционала, называемого «действием». Принцип наименьшего действия Мопертьюи оказался связан с принципом минимального времени Ферма, сформулированным за сто лет до этого. Позднее были открыты и другие вариационные принципы: принцип наименьшего действия Гаусса, принцип виртуальных перемещений Лагранжа, принцип Гамильтона-Остроградского и т.д. Сначала вариационные принципы были открыты в механике, затем в электродинамике и других областях физики. Оказалось, что все основные уравнения, которыми оперирует физика, определяют траектории, являющиеся экстремалями некоторых функционалов. Т.о. если задан функционал, очень просто по нему записать систему уравнений динамики, приравняв нулю его первую производную по времени. Функционал при этом является первым интегралом этих уравнений, т.е. сохраняющейся величиной, которая задает геометрию или фазовый портрет системы. Уравнения, описывающие динамику системы вдоль данных траекторий , называются уравнениями Эйлера. Можно сказать, что все уравнения физики являются уравнениями Эйлера. И каждое из них скрывает (или раскрывает) закон сохранения некоторого функционала. Т.е. законы физики – это законы сохранения некоторых величин.
Согласно теореме Э. Нетер, каждому закону сохранения соответствует определенная симметрия системы. Это можно понимать так, что каждая сохраняющаяся величина задает геометрию, в которой реализуется физика, описываемая уравнениями Эйлера. Геометрия и физика оказываются дополнительными дург другу: чем ближе модель геометрии системы к истинной геометрии системы, тем проще представление динамики (или физики) системы. Эйнштейн впервые свел физику к геометрии в теории гравитации. Позднее его подход развил Г. Крон для описания электрических сетей и машин: в сложной геометрии его тензорных сетей от физики оставалось только элементарное уравнение Ома. В современных теориях геометрия всё более «впитывает» в себя физику. Геометрическим пределом такого подхода явилась геометродинамика Дж. Уилера, в которой физические явления строятся из свойств пространства-времени. Она гласит: «в мире нет ничего, кроме пустого искривленного пространства. Материя, заряд, электромагнитные и другие физические тела являются лишь проявлением искривленного пространства. Физика есть геометрия. Все физические понятия должны быть представлены с помощью пустого, различным образом искривленного пространства... Масса, время, длина, электромагнитные поля... являются объектами чистой геометрии..». Напомним, что после теории относительности под «пространством» понимается хронотоп или пространство-время. Поэтому речь должна идти о геометрии хронотопов.
Существует изящный способ геометризации физических величин – запись их через их размерности с последующим сведением этих размерностей к размерностям длины и времени. Например, приравняв размерности силы из второго закона Ньютона и закона всемирного тяготения, можно выразить размерность массы через размерность длины и времени: [m] = [L3T-2] . Теперь можно свести к той же форме записи выражения для импульса, энергии, силы, а через них выразить и электрические величины. Эта идея позволила Р.О.ди Бартини свести всевозможные законы сохранения в природе в «таблицу законов природы» в форме [ Ln Tm ] , где L – переменная размерности длины, а T – переменная размерности времени, степени n и m пробегают всевозможные целые значения от - ∞ до +∞. (см. Рис. 1). По сути дела каждый такой закон сохранения вида [ Ln Tm ] представляет собой хронотоп или «тело времени» выбранного явления. В этом хронотопе и осуществляется динамика, описываемая соответствующими уравнениями Эйлера. Такой подход позволяет рассматривать все системы как системы транспортировки тех или иных величин, т.е. как структуры потоков или «диссипативные структуры» (И.Пригожин), а само движение понимать как преобразование координат с инвариантом из таблицы физических величин Р.О. ди Бартини.
Все физические величины в таблице ди Бартини связаны между собой посредством операций интегрирования и дифференцирования (см. Рис.2). Это означает, что приняв некоторую величину из таблицы ди Бартини за сохраняющийся функционал, мы можем записать уравнение Эйлера для величины, стоящей на одну клетку выше или правее (поскольку речь идет о взятии производной) на Рис.2. Еще Лебниц говорил, что интегрирование увеличивает число измерений, а дифференцирование – уменьшает. Ньютон считал, что линия получается при движении точки, поверхность – при движении линии, тело – при движении поверхности. Как раз это возрастание размерности величин мы и видим в выделенном столбце на Рис.2 , где происходит интегрирование по скорости.
Рис.1. Таблица законов природы Р.О. ди Бартини (из книги В.В. Дружинина и Д.С. Конторова «Системотехника», 1985)
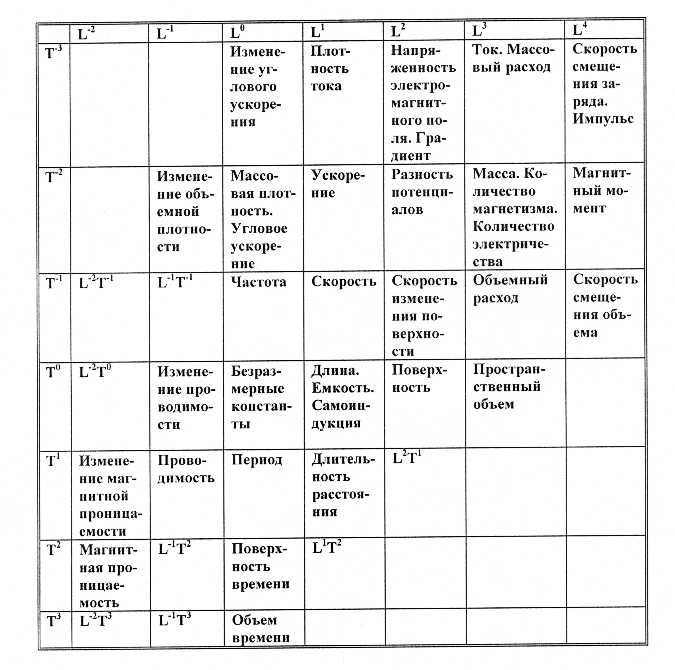
Рис.2. Таблица переходов между законами природы (из книги В.В. Дружинина и Д.С. Конторова «Системотехника», 1985)
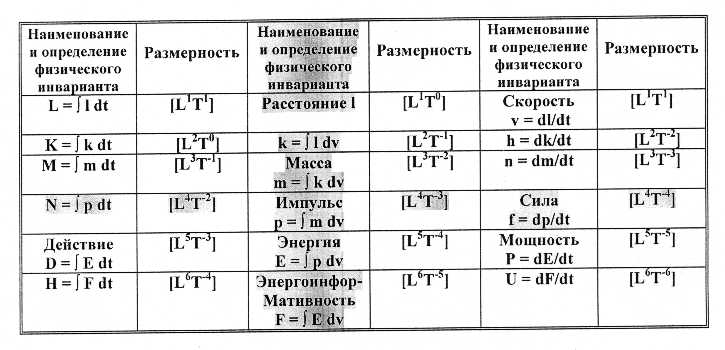
Мой учитель Д.В. Осадчий (см. о нем в эссе «Рассуждение о методе...») понимал интегрирование как операцию «наполнения границы», а дифференцирование как операцию «взятия границы». Жак Деррида понимал операцию «Differance» как деконструкцию целостности. Тогда операция интегрирования предстает в облике конструирования нового из готовых блоков старого. В топологии подобным образом составляется комплекс из симплексов. «Совокупность симплексов вместе с их границами, т.е. симплексами меньших размерностей, образует комплекс». Для изучения комплексов А. Пуанкаре ввел группы гомологий, определение которых основано на т.н. отношении инцидентности или «вложения» (Осадчий), т.е. знании того, входит или нет какой-нибудь один симплекс в состав границы другого симплекса. Пространства симплексов образуют гомологическую последовательность, которую Д.В. Осадчий назвал «гомологической структурой». На Рис.3 изображена гомологическая структура трехмерного симлекса – тетраэдра. Если, как это делал Осадчий, обозначить точку через Т1 (Т – от слова «Точка»), длину через Т2, поверхность через Т3, объем через Т4, то Рис.3 иллюстрирует известные правила интегрирования – дифференцирования:
∂TN/∂T = NTN-1 ∫ NTN-1 dT = TN
В частности, ∂Т4/∂Т = 4Т3 означает, что граница тетраэдра состоит из четырех элементов поверхности – треугольников. И, наоборот, «заполнение» конструкции из четырех треугольников по формуле ∫ 4T3 dT = T4 даст объем тетраэдра.
Рис.3. Отношение вложения симплексов разной размерности.
Гомология понимается в математике как «формализация интуитивного представления об ограниченности множеств» или, можно сказать, о «замыкании множеств»: гомология – это формализация свойства «быть границей». Граница некоторого множества гомологична этому множеству. Тогда последовательность гомологий или гомологическая структура может рассматриваться как система вложенных друг в друга границ наподобие русской матрешки. Если в гомологической структуре «старшая граница сохраняется, то … такая система имеет возможность перераспределять свои младшие границы» (Осадчий). В частности, объем может выступать в ипостасях различных платоновых тел, гомологическая структура младших границ которых отличается друг от друга. Так, гомологическая структура тетраэдра может быть записана в виде: 1Т4 + 4Т3 + 6Т2 + 4Т1 + 1Т0 , что означает – один элемент объема, четыре элемента поверхности, шесть элементов длины, четыре точки и пустота (последняя добавлена по формальным соображениям). Гомологическая структура куба будет 1Т4 + 6Т3 + 12Т2 + 8Т1 + 1Т0 . Гомологическая структура октаэдра будет 1Т4 + 8Т3 + 12Т2 + 6Т1 + 1Т0 . Гомологическую структуру икосаэдра и додекаэдра можете записать самостоятельно (в качестве упражнения). Во всех этих формулах старшая граница (член высшей размерности) остается неизменной, а младшие границы изменяют свой вес. Это делает наглядным содержание вариационного принципа. Требование минимизации функционала «действие», который играет роль старшей границы Тn, позволяет записать уравнения Эйлера для динамики на уровне Тn-1. По словам Д.В. Осадчего: «Во временных процесах абсолютное пространство (задаваемое старшим членом Tn ) можно выключить из гомологической суммы, описывающей структуру времени данного уровня, т.к. оно не изменяется. Важнейшим для нас является член Tn-1 - именно по этому члену мы определяем ход процесса». Мы возвращаемся к метафоре Платоновой пещеры, в которой мы обречены наблюдать лишь динамику теней-проекций на стене – (младшей) границе реальности. Сама же реальность присутствует в нашем знании в виде законов сохранения величин из таблицы ди Бартини.
Коэффициенты в записи гомологической струтуры симплексов различной размерности совпадают с коэффициентами биномиального разложения (а + в)N при различных N. Эти коэффициенты образуют т.н. треугольник Паскаля, который до Паскаля знали и китайцы, и индийцы, и Омар Хаям. На Рис.4. изображен треугольник Паскаля, по которому вы можете самостятельно записать гомологическую стуктуру симплекса соответствующей размерности. Симплексы до трехмерного включительно изображены слева от треугольника. (Говорят, что можно вообразить и четырехмерный симплекс, состоящий из пяти тетраэдров. Во всяком случае его проекция на плоскость представляет собой пятиугольник с вписанной в него звездой). Последовательность усложняющихся симплексов – это образ времени-конструкции (как называл его Поль Валери): новое возникает в результате вложения новой старшей границы (размерность которой на единицу выше размерности текущей старшей границы) путем образования из набора симплексов текущей размерности «оболочки», способной «охватить» или «вместить» новую старшую границу. Д.В. Осадчий назвал эту последовательность вложений «временем-организацией». Интересно, что время-организация посредством одного любопытного свойства треугольника Паскаля проецируется на широко наблюдаемое в органической природе «спиральное время» (см. о спиральном времени в моем эссе «Морфология чисел»). Если суммировать числа, образующие треугольник Паскаля, по «диагонали треугольника», то мы получим ряд Фибоначчи (Рис.4, справа). Числа из ряда Фибоначчи повсеместно встречаются в морфологии растений: «Черенки листьев различных растений примыкают к стеблю по спирали через 1/3 полного оборота – у орешника, 2/5 – у дуба, 3/8 – у тополя и груши, 5/13 – у ивы, чешуйки на еловой шишке, ячейки на ананасе и семена подсолнечника расположены спиралями, причем количества спиралей каждого направления также являются числами Фибоначчи». Т.о. те морфологические закономерности, которые мы привыкли видеть вокруг себя в живой природе сигнализируют нам о наличии организации, базирующейся на динамике вложения или конструктивного освоения среды обитания. Ж. Пиаже называл такой акт вложения «адаптацией». Последняя состоит из двух актов – «ассимиляции» и «аккомодации». Первый осуществляет вложение («интериоризацию» по Пиаже) части среды обитания в «организм», превращение ее в новый «орган» организма. Второй заключается в перенастройке всех остальных систем организма, дабы их активность не мешала активности нового «органа». «Орган» здесь понимается скорее в физиологическом смысле китайской медицины, нежели в анатомическом смысле европейской научной традиции. Китайский «орган» эквивалентен «функциональной системе» П.К.Анохина. Таким образом, организация, изображаемая гомологической структурой, представляет собой «анатомию» младших границ с «физиологией» старшей границы, если пользоваться терминами биологии. А как эта организация будет выглядеть в терминах физики?
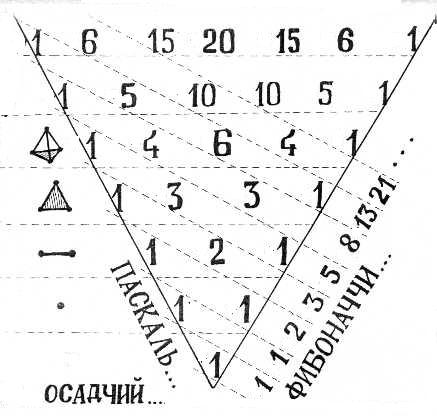
Рис.4. Треугольник Паскаля с соответсвием его строк гомологической структуре симплексов (слева) и ряду Фибоначчи (справа).
В теоретической физике удобно изображать динамику систем в переменных «действие-угол». Фазовое пространство системы в этих переменных представляет собой тор, описываемый инвариантным вектором «действия». Траектория системы навивается на тор с густотой (частотой), задаваемой производной переменной «угол» по времени. Такие инвариантные (по переменной «действие») торы называются КАМ-торами (по первым буквам теории Колмогорова – Арнольда – Мозера). «В процессе движения траектория остается всё время на торе. Поэтому говорят о существовании инвариантных торов… Изменением интегралов движения получаем семейство инвариантных торов». Это семейство образует иерархию адиабатических инвариантов, если выполняется условие адиабатического приближения – достаточная разнесенность масштабов собственных времен движения на отдельных торах.Таким образом, многообразие систем, характеризующихся различными инвариантами, представляется набором инвариантных торов, которые образуют подобие гомологической структуры времени: на каждом из таких торов задано собственное время-дление, характеризуемое определенным набором частот. Но исчерпывается ли все фазовое пространство множеством КАМ-торов? Л.Д. Ландау в своей теории турбулентности исходил из того, что такие торы плотно заполняют все фазовое пространство. В 60-е годы ХХ века стало ясно, что это не так. Д. Рюэль и Ф. Такенс показали, что при заполнении фазового пространства КАМ-торами обязательно останется область неупорядочиваемого посредством них пространства. В этой области динамика системы характеризуется так называемым «странным аттрактором» (Рис. 5).
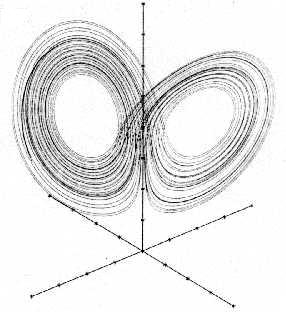
Рис.5. Странный аттрактор Лоренца.
Странный аттрактор содержит область, где траектории близко подходят одна к другой, поэтому малейшие возмущения, всегда присутствующие в реальной системе, легко и непредсказуемо перебрасывают систему с одной детерминистской траектории на другую. Изображающая систему точка случайным образом оказывается на левом или правом «ухе» аттрактора Лоренца (Рис. 5). Если попытаться изобразить такую динамику в виде тора, то единственным подходящим кандидатом для этого будет тор, впервые рассмотренный Ф. Клейном и названный им «эллиптической геометрией». Это тор, дырка которого стянута в точку, багодаря чему все траектории, навивающиеся на этот тор, будут пересекаться в этой центральной точке. Я назвал такой тор «Кляйн-тором» в честь автора, но еще и потому, что по-немецки это значит «маленьктй тор», а он действительно «меньше» нормального КАМ-тора благодаря отсутствию дырки (Рис. 6).
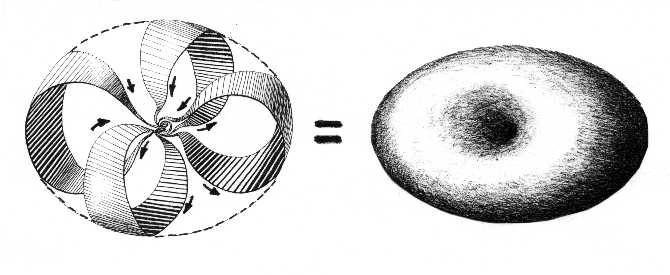
Рис.6. Кляйн-тор: справа внешиний вид, слева – траектории на торе.
Если сравнить Рис.5 и Рис.6, нетрудно заметить, что траектории аттрактора Лоренца предсталяют собой сечение Кляйн-тора. Центральная точка Кляйн-тора является наглядным образом так называемой «слипшейся» или «незамкнутой» точки. Эти «нехаусдорфовы» или «неевдоксовы» точки впервые начал рассматривать в 60-е годы ХХ века А. Гротендик. Сам Кляйн-тор является замыканием этой точки. Но не только он сам. Если Кляйн-тор является обязательным дополнением в попытке заполнить фазовое пространство КАМ-торами, то вся система вложенных КАМ-торов вокруг Кляйн-тора будет замыканием его незамкнутой центральной точки. Получится конструкция, которая эквивалентна гомологической структуре, о которой мы говорили выше (Рис.7). Старшая граница изображается Кляйн-тором, младшие границы – КАМ-торами.
На КАМ-торе переменные действия являются инвариантами движения (производная от действия по времени равна нулю). Такие системы А. Пуанкаре назвал интегрируемыми. Интегрируемость означает возможность расссматривать движение изображающей точки на отдельном торе независимо от движений на других торах. Фактически это означает, что КАМ-тор изображает вариационный принцип, о котором мы говорили в начале эссе: действие играет роль функционала, а производная по времени от переменной угол задает «Эйлеровы уравнения» динамики. Т.е. мир классической физики – это мир, целиком расположенный на КАМ-торах. Но, как мы говорили выше, КАМ-торы не заполняют собой весь реальный мир. Более того, «в конце XIX в. Брунс и Пуанкаре доказали, что большинство динамических систем … неинтегрируемы». Неинтегрируемость системы автоматически означает наличие в ней хаоса. В ХХ веке стало ясно, что «почти все динамические системы имеют область хаоса. И наоборот, системы, которые имеют только регулярную динамику, представляют собой исключительные случаи». Мир представляет собой океан хаоса с островами порядка (Г.М. Заславский). И острова эти являются КАМ-торами.
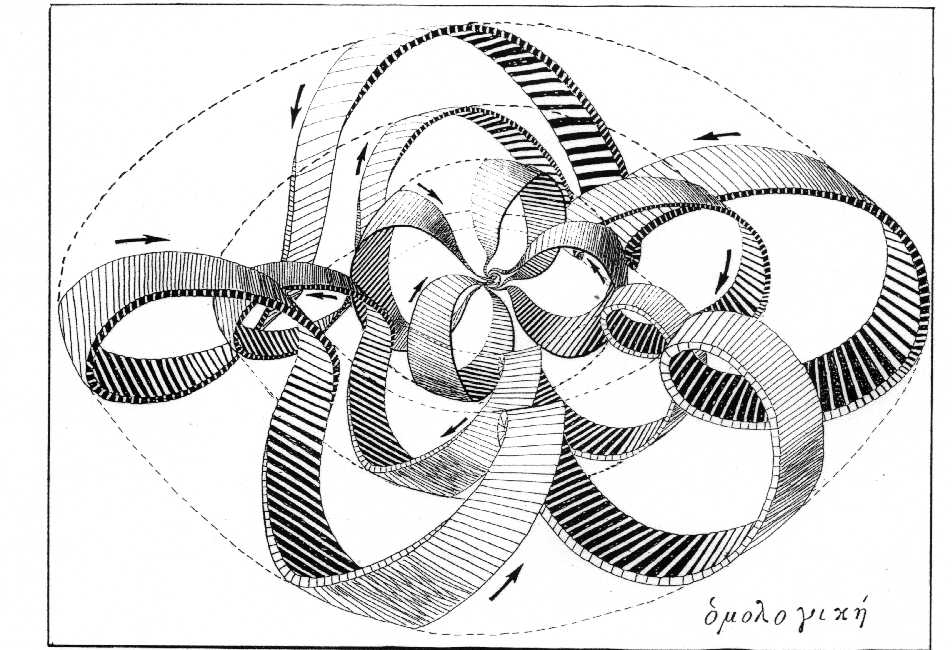
Рис.7. Гомологическая структура вложенных торов.
Теория КАМ показала, что фазовое пространство в результате действия малого возмущения распадается на области упорядоченного движения (инвариантные торы) и разделяющие эти области границы, которые «могут, соединяясь , пронизывать все фазовое пространство». Возникает т.н. «стохастическая паутина» или «паутина Арнольда», которая охватывает области упорядоченного движения – КАМ-торы, объединяя их в единое целое. Частица , попавшая в область стохастической паутины, может сколь угодно далеко уйти по ней. Это явление называется «диффузией Арнольда». Дрейф частицы вдоль паутины Арнольда «можно назвать динамической организацией». Области каналов паутины играют роль сепаратрис, разделяющих КАМ-торы. Вдоль этих каналов течет время хаоса, которое ортогонально механическому времени динамики на КАМ-торе. По этим каналам можно перейти с одного КАМ-тора на другой, т.е. с одного «закона сохранения» (инварианта «действие») на другой. (Для тех, кто читал мое эссе «Морфология чисел», скажу, что движение на КАМ-торе соответвует движению изображающего вектора вдоль конуса возведения алгебраического числа в алгебраическую степень (Рис. 7 в указанном эссе), переходы же между торами – это возведение кватерниона в кватернионную степень (Рис. 10 в указанном эссе)). Это и есть переход из одной клетки таблицы ди Бартини в другую, который осуществляется, как мы показали выше, посредством операций интегрирования-дифференцирования (см. Рис.2). Какой изящный парадокс: интегрирование осуществляет неинтегрируемая система! Паутина Арнольда осуществляет акомодацию (Ж.Пиаже) КАМ-торов в единой организации. Но каков механизм ассимиляции (Ж.Пиаже) новой старшей границы из океана хаоса в архипелаг островов порядка - гомологическую структуру? Или, другими словами, как происходит превращение неинтегрируемой системы в интегрируемую?
Это делает Кляйн-тор. Мы говорили выше, что он является образом динамики странного аттрактора. По определению Дж. Николиса странный аттрактор является устройством, сжимающим информацию. Т.е. странный аттрактор – это область хаоса, способная упорядочивать другие области хаоса. Такой акт упорядочивания или превращение Кляйн-тора в КАМ-тор изображено на Рис. 8.
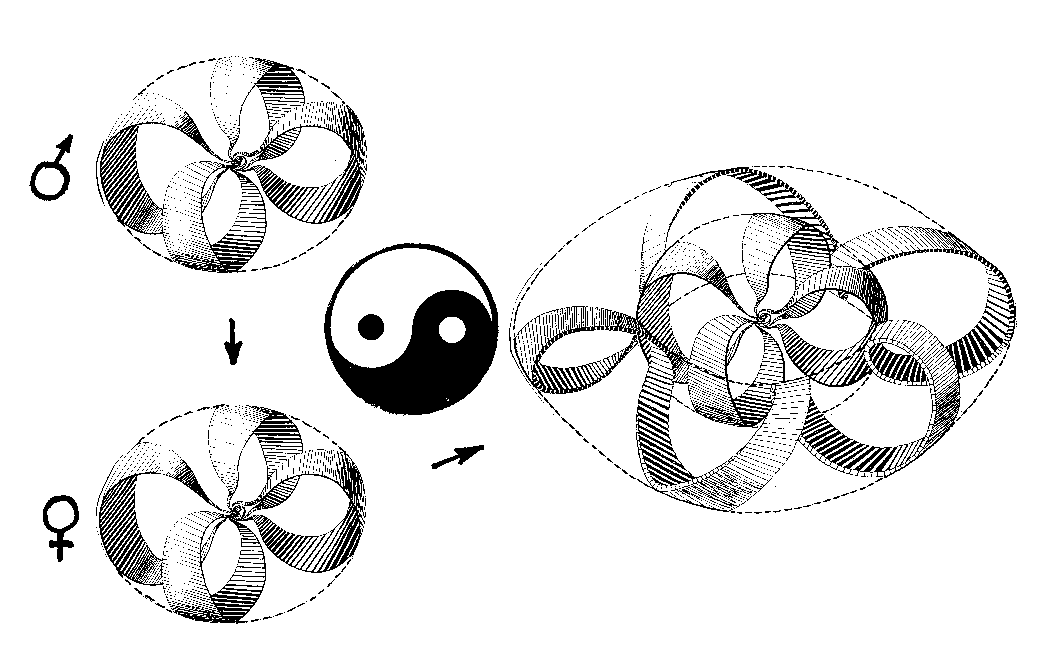
Рис. 8. «Космическая дефлорация» - превращение Кляйн-тора в КАМ-тор путем вложения другого Кляйн-тора.
Старшая граница гомологической структуры (Рис.7) «затягивает» в себя (А.М. Молчанов) часть среды обитания (на Рис.8 она тоже представлена Кляйн-тором), которая становится новой старшей границей. Прежняя старшая граница превращается в КАМ-тор, т.е. становится младшей границей гомологической структуры (центральная точка Кляйн-тора превращается в дырку, заполненную новым Кляйн-тором. Этот аспект динамики представлен в древнекитайском символе «Инь-Ян» в виде маленькой области одного знака в большой области противоположного знака – см. в центре Рис.8). Произошло то, что Д.В. Осадчий называл «вложением» (сексуальные ассоциации здесь вполне уместны). Последовательность таких актов вложения составляет течение «творческого» времени А. Бергсона, которое И. Пригожин назвал «временем-историей», а Д.В. Осадчий – «временем-организацией».
Таким образом, таблица ди Бартини обретает онтологический статус: ее клетки – это КАМ- или Кляйн-торы, а границы между клетками – это паутина Арнольда. Три типа времени демонстрирует нам эта таблица: время-дление механики в выделенных КАМ-торах-клетках, термодинамическое время-диффузия вдоль паутины Арнольда, и время-организация переходов между клетками, выражаемое операциями интегрирования-дифференцирования. Но почему иные клетки этой таблицы законов природы мы изображаем КАМ-торами, а иные Кляйн-торами? Какое различие существует между ними?
Кляйн-тор – это образ неалгоритмизируемой динамики. Н.А. Бернштейн, классифицируя объекты математики, выделил два типа алгоритмов, которые назвал алгоритмами первого и второго рода. Первые можно выразить формулой, вторые можно выполнить только шаг за шагом, но единой формулой они невыразимы. С. Уолфрэм назвал такие системы «вычислительно неприводимыми». Выражаясь более образно, можно сказать, что алгоритмы первого рода – это знание, а алгоритмы второго рода – это бытие, которое мы не можем (пока) заменить знанием и обречены его реально проживать. В нашей таблице законов природы знание как раз и выражается КАМ-торами и известными формулами интегрирования-дифференцирования, описывающими переходы между ними. Кляйн-тор – это область бытия, которое еще не освоено нашим знанием. Чтобы «удержаться» в соответствующей клетке таблицы ди Бартини, мы должны совершать волевое усилие, организующее все наши прежние достижения (выражаемые гомологической структурой КАМ-торов) – это усилие и есть «интегрирование» неинтегрируемой системы. С. Лем удачно назвал такую реальность «технологией», в отличии от «закона», выражающего устоявшееся знание. Г. Крон называл то же самое «организацией» или «обобщенной машиной», которой, в частности, может быть и организм. Т.е. двигаясь от начала таблицы ди Бартини вглубь ее бесконечности, мы постепенно встречаем вместо привычных в классической физике законов сохранения массы, энергии, заряда, импулса и т.п. странные закономерности, которые казалось бы противоречат уже известным законам и встречаются в весьма экзотических условиях. Такими условиями являются сложноорганизованные хронотопы, в роли которых могут выступать и машины, построенные человеком, и сами организмы. Это и есть «технологии» Лема. Например, такой «технологией» является атомная организация сверхпроводника, приводящая к исчезновению сопротивления току, такой «технологией» является теплообменник в ластах тюленя, который позволяет передавать тепло от одного тела к другому почти со 100% эффективностью, что противоречит интуитивному представлению о поведении тел в соответствии со вторым началом термодинамики. Такой «технологией» является вибрация маятника в точке подвеса, которая неожиданно делает устойчивым его положение, направленное вертикально вверх. Я хочу сказать, что где-нибудь в таблице ди Бартини при достаточно больших n и m [LnTm] будет задавать некторую «технологию» Лема или «машину» Крона, а при еще больших n и m [LnTm] будет описывать закономерность устройства организма, а еще дальше мы встретимся с некоторыми инвариантами произведений человеческого духа – искусства, философии, религии. Ведь что такое, в конце концов, человеческая культура, как ни система запретов-табу – это ведь тоже некий закон сохранения. Платон, прозревая свой мир эйдосов, бродил своим разумом где-то в дали клеток таблицы ди Бартини.
В 1992 году я встретил в Ялте интересного физика-теоретика Г.В. Рязанова. Он мне рассказал о своей гипотезе устройства нашего мироздания. Мир, согласно Рязанову, представляет собой дополнительность двух миров – мира физики и «мира ангелов». То, что в первом является физикой, во втором является этикой, и наоборот. Сейчас, обращаясь к таблице законов природы, можно уточнить это представление. Если поставить ножку циркуля в начало таблицы ди Бартини и провести окружность, то все клетки, попавшие внутрь ее, будут изображаться КАМ-торами. Это мир физики. Для этого мира все клетки, которые не попали внутрь окружности должны изображаться Кляйн-торами. Для мира физики это область этики: здесь инварианты задаются как усилия воли – в физиологии это называется «установка» (Д.И. Узнадзе), «доминанта» деятельности (А.А. Ухтомский) или «акцептор потребного будущего» (П.К. Анохин), в этике это называется «категорическим императивом Канта», «табу» первобытных народов, «заповедями» Моисея. И напротив, для «мира ангелов» ножка их циркуля будет стоять в точке «бесконечность», а окружность будет совпадать с границей мира физики. Для ангелов вся наша этика будет изображаться КАМ-торами (поэтому ангелы не умеют грешить – они не могут сойти с рельсов своей добродетельной или злой, в зависимости от ангельского департамента, физики), но наша физика – внутренность нашей окружности – будет для них состоять из Кляйн-торов. Это значит, что наши законы физики могут ими нарушаться, и мы будем наблюдать эти нарушения в виде различных чудесных явлений (вроде «ведьминых кругов» на полях).
А человек – пограничное существо. Он всегда располагается на самой окружности, частью своей принадлежа миру физики, которую он познает и описывает в виде КАМ-торов, а частью своей принадлежа миру этики, изображаемой Кляйн-торами. В этом мире этики он страдает, совершает подвиги, грешит, т.е. обладает бытием, которое только усилием всей его жизни превращается в знание, усваиваемое следующими поколениями людей в виде КАМ-тора. Тем самым увеличивается радиус окружности мира физики, но не становится от этого меньше мир этики – для следующих поколений всегда остается простор для того, чтобы страдать, грешить и совершать подвиги.
Теперь мы можем интерпретировать древнекитайский символ «Инь-Ян» как дополнительность областей КАМ- и Кляйн-торов (Рис.9). Граница между ними постоянно меняется – области Кляйн-торов и КАМ-торов взаимно-превращаются друг в друга в зависимости от принятия «физической» или «ангельской» точки зрения. Изменение этой границы демонстрирует нам течение времени-организации через клетки таблицы законов природы ди Бартини.

Рис.9. Инь-Ян |
Дата: 15.10.2005, Просмотров: 8522
|
|
|

